Question

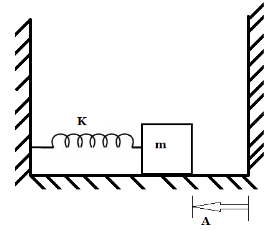
In the figure shown the spring is in a relaxed position. Now the spring is compressed by $ 2\;A $ and released. A mass $ m $ attached with the spring collides with the wall and loses two-thirds of its kinetic energy and returns. Find the time after which the spring will have maximum compression after releasing. (Neglect Friction).

(A) $ \dfrac{{7\pi }}{{12}}\sqrt {\dfrac{m}{K}} $
(B) $ \dfrac{{17\pi }}{2}\sqrt {\dfrac{m}{K}} $
(C) $ \dfrac{{17\pi }}{{12}}\sqrt {\dfrac{m}{K}} $
(D) $ \dfrac{{7\pi }}{{12}}\sqrt {\dfrac{{{m^2}}}{K}} $

Answer 1

Hint: Here we shall conserve energy before the collision and find the kinetic energy of the mass just before the collision. After that, we will conserve the energy after the collision with the new reduced kinetic energy and find the maximum compression of the spring from it. Then we will form two separate equations of a general S.H.M. to get the separate equations of motion before and after the collision.

Complete Step by step solution
Here since the frictional forces are not taken into account we will conserve energy till before the first collision to calculate the kinetic energy of the mass just before the first collision.
Thus initial potential energy when the spring was compressed by $ 2\;A $ is given by $ \dfrac{1}{2}K{x^2} $ , where $ K $ is the spring constant and $ x $ is the compression in the spring which here is equal to $ 2\;A $ .
The initial kinetic energy of the block is zero since it is released from rest.
The final kinetic energy of the block needs to be calculated.
The final potential energy in the spring is given by $ \dfrac{1}{2}K{x^2} $ , where $ K $ is the spring constant and $ x $ is the expansion in the spring which here is equal to $ A $ as shown in the diagram.
Thus by conservation of energy, we get,
Initial K.E. + Initial P.E. = Final K.E. + Final P.E.
 $ \Rightarrow 0 + \dfrac{1}{2}K{(2A)^2} = K.E{._{final}} + \dfrac{1}{2}K{A^2} $
 $ \Rightarrow K.E{._{final}} = \dfrac{3}{2}K{A^2} $
It is given in the question that after the collision, two-thirds of the kinetic energy is lost. Therefore the remaining kinetic energy left is equal to $ \dfrac{1}{2}K{A^2} $ with the velocity directed in the opposite direction.
Now again we will apply conservation of energy and get the following equation
 $ \Rightarrow \dfrac{1}{2}K{A^2} + \dfrac{1}{2}K{A^2} = 0 + \dfrac{1}{2}K{x^2} $ ,
where $ x $ is the final compression of the spring when the block comes to rest.
Thus we get
 $ \Rightarrow x = \sqrt 2 A $ ,
which is the maximum compression of the spring.
Now we will have to assume the motion of the spring as that of a simple harmonic motion.
We consider the general equation of the motion as
 $ y = D\sin (\omega t - \phi ) $ ,
where $ D $ is the maximum displacement of the mass,
 $ \omega = \sqrt {\dfrac{K}{m}} $ and $ \phi $ is the phase difference as chosen carefully.
We will use the initial conditions to get the equations of the motions.
For the motion with a displacement of $ 2\;A $ , we get $ y = - 2A $ and $ \phi = \dfrac{\pi }{2} $ for $ t = 0 $ . Thus the equation becomes
 $ {y_1} = 2A\sin (\sqrt {\dfrac{K}{m}} {t_1} - \dfrac{\pi }{2}) $ .
When we use this equation at $ {y_1} = A $ , i.e. at the point of collision, we get
 $ \Rightarrow A = 2A\sin (\sqrt {\dfrac{K}{m}} {t_1} - \dfrac{\pi }{2}) $
 $ \Rightarrow {\sin ^{ - 1}}\dfrac{1}{2} = \sqrt {\dfrac{K}{m}} {t_1} - \dfrac{\pi }{2} $
On further simplifying we will get,
 $ \Rightarrow \dfrac{\pi }{6} = \sqrt {\dfrac{K}{m}} {t_1} - \dfrac{\pi }{2} $
 $ \Rightarrow \dfrac{\pi }{6} + \dfrac{\pi }{2} = \sqrt {\dfrac{K}{m}} {t_1} $
Taking $ {t_1} $ as the subject of the equation we get,
 $ \Rightarrow {t_1} = \dfrac{{2\pi }}{3}\sqrt {\dfrac{m}{K}} $ .
This is the time after release at which the block collides with the wall.
Now for the return journey of the block, we will use another S.H.M. equation where the maximum displacement is $ \sqrt 2 A $ as calculated above. This the displacement after the collision when the spring is compressed to its maximum.
Here we will frame the equation of the S.H.M. as if the block has started from its displacement of $ \sqrt 2 A $ and is going to collide with the wall. Since we have to calculate the time, the answer will be the same. Now for the motion with a displacement of $ \sqrt 2 A $ , we get $ y = - \sqrt 2 A $ for $ t = 0 $ and $ \phi = \dfrac{\pi }{2} $ . Thus the S.H.M. equation becomes
 $ {y_2} = \sqrt 2 A\sin (\sqrt {\dfrac{K}{m}} {t_2} - \dfrac{\pi }{2}) $ .
When we use this equation at $ {y_2} = A $ , i.e. at the point of collision, we get
 $ \Rightarrow A = \sqrt 2 A\sin (\sqrt {\dfrac{K}{m}} {t_2} - \dfrac{\pi }{2}) $
 $ \Rightarrow {\sin ^{ - 1}}\dfrac{1}{{\sqrt 2 }} = \sqrt {\dfrac{K}{m}} {t_2} - \dfrac{\pi }{2} $
We know that $ {\sin ^{ - 1}}\dfrac{1}{{\sqrt 2 }} = \dfrac{\pi }{4} $ ,
 $ \Rightarrow \dfrac{\pi }{4} = \sqrt {\dfrac{K}{m}} {t_2} - \dfrac{\pi }{2} $
After further simplification,
 $ \Rightarrow \dfrac{\pi }{4} + \dfrac{\pi }{2} = \sqrt {\dfrac{K}{m}} {t_2} $
 $ \Rightarrow {t_2} = \dfrac{{3\pi }}{4}\sqrt {\dfrac{m}{K}} $ .
To get the total time taken for the first maximum compression of the spring after releasing the block, we will add the two time intervals calculated above, i.e. $ {t_1} + {t_2} $ .
 $ \Rightarrow {t_1} + {t_2} = \dfrac{{2\pi }}{3}\sqrt {\dfrac{m}{K}} + \dfrac{{3\pi }}{4}\sqrt {\dfrac{m}{K}} $
 $ \Rightarrow t = \dfrac{{17\pi }}{{12}}\sqrt {\dfrac{m}{K}} $ .
Thus the answer is option (C).

Note
Here we will consider the motion of the spring as a simple harmonic motion, or an S.H.M. Therefore it becomes easier to form the equation of any S.H.M. from its general form of $ \dfrac{{{d^2}y}}{{d{t^2}}} + \dfrac{K}{m}y = 0 $ . Here we have taken the equation to be $ y = D\sin (\omega t - \phi ) $ . In general, any sinusoidal equation is a valid solution of the above differential with proper constants and phase.