Question

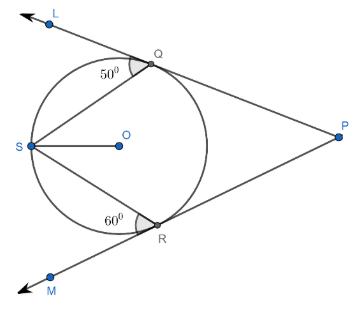
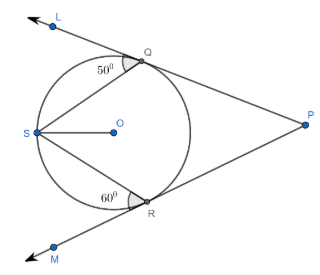
In the figure, PQ and PR are tangents to the circle with center O and S is a point on the circle such that, $\angle SQL=50$ degree and $\angle SRM=60$ degree. Find $\angle QSR$.

Answer 1

Hint: For solving this question, first we will see that angles opposite to equal sides of an isosceles triangle are equal and tangent to the circle is perpendicular to the radius of the circle at the point of contact. Then, we will use them to find the measure of $\angle OSQ$ and $\angle OSR$. Then further, we will write $\angle QSR=\angle OSQ+\angle OSR$ and substitute suitable values to get the correct answer for this question.

Complete step-by-step solution -
Given:
In the figure, PQ and PR are tangents to the circle with center O and S is a point on the circle such that, $\angle SQL=50$ degree and $\angle SRM=60$ degree. And we have to find the measure of $\angle QSR$.
 

Now, before we proceed we will see an important property related to isosceles triangles.
Isosceles Triangle Property:
Angles opposite to equal sides of an isosceles triangle are equal. This can be understood with the help of the figure below:

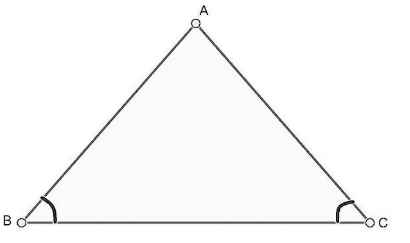
In the above figure, $\Delta ABC$ is shown in which $AB=AC$. Then, $\angle ABC=\angle ACB$.
Now, before we proceed, we should know the following important theorem of the circle:
Tangent Theorem:
Statement: The tangent to the circle is perpendicular to the radius of the circle at the point of contact. For more clarity, look at the figure given below:

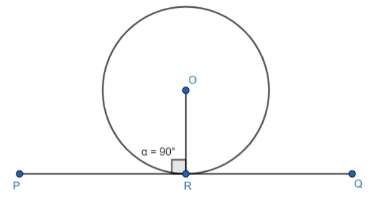
In the above figure, PQ is a tangent at point R on the circle and $\angle ORP=\angle ORQ={{90}^{\circ }}$.
Now, we will be using the above theorems to solve this question.
As we have the following figure:

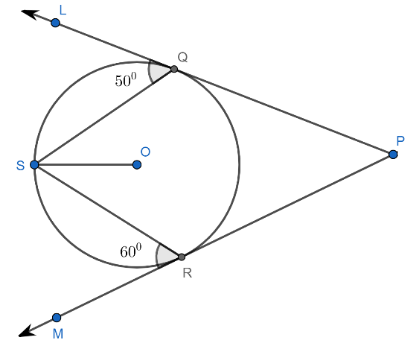
Now, we joint the points O & Q, O & R. For more clarity, look at the figure given below:

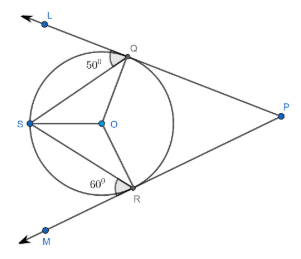
Now, in the above figure, S, R and Q are points on the circle with centre O. Then,
$OS=OQ=OR=\text{ radius}..............\left( 1 \right)$
Now, from the above result we conclude that in $\Delta OQS$ , length of side OS is equal to OQ so, $\Delta OQS$ will be an isosceles triangle. Moreover, in $\Delta OSR$ , length of side OS is equal to OR and as we know that, angles opposite to equal sides of an isosceles triangle are equal. Then,
$\begin{align}
  & \angle OSQ=\angle OQS........\left( 2 \right) \\
 & \angle OSR=\angle ORS.........\left( 3 \right) \\
\end{align}$
Now, as we know that, tangent to the circle is perpendicular to the radius of the circle at the point of contact. Then,
$\angle OQL=\angle ORM={{90}^{\circ }}..............\left( 4 \right)$
Now, we will write $\angle OQL=\angle OQS+\angle SQL$ and it is given that, $\angle SQL={{50}^{\circ }}$ . Then,
$\begin{align}
  & \angle OQL=\angle OQS+\angle SQL \\
 & \Rightarrow \angle OQL=\angle OQS+{{50}^{\circ }} \\
 & \Rightarrow \angle OQS=\angle OQL-{{50}^{\circ }} \\
\end{align}$
Now, we will substitute $\angle OQL={{90}^{\circ }}$ from equation (4) in the above equation. Then,
$\begin{align}
  & \angle OQS=\angle OQL-{{50}^{\circ }} \\
 & \Rightarrow \angle OQS={{90}^{\circ }}-{{50}^{\circ }} \\
 & \Rightarrow \angle OQS={{40}^{\circ }}...............\left( 5 \right) \\
\end{align}$
Now, we will write $\angle ORM=\angle ORS+\angle SRM$ and it is given that, $\angle SRM={{60}^{\circ }}$ . Then,
$\begin{align}
  & \angle ORM=\angle ORS+\angle SRM \\
 & \Rightarrow \angle ORM=\angle ORS+{{60}^{\circ }} \\
 & \Rightarrow \angle ORS=\angle ORM-{{60}^{\circ }} \\
\end{align}$
Now, we will substitute $\angle ORM={{90}^{\circ }}$ from equation (4) in the above equation. Then,
$\begin{align}
  & \angle ORS=\angle ORM-{{60}^{\circ }} \\
 & \Rightarrow \angle ORS={{90}^{\circ }}-{{60}^{\circ }} \\
 & \Rightarrow \angle ORS={{30}^{\circ }}...............\left( 6 \right) \\
\end{align}$
Now, we will substitute $\angle OQS={{40}^{\circ }}$ from equation (5) into equation (2) and $\angle ORS={{30}^{\circ }}$ from equation (6) into equation (3). Then,
\[\begin{align}
  & \angle OSQ={{40}^{\circ }}..........\left( 7 \right) \\
 & \angle OSR={{30}^{\circ }}...........\left( 8 \right) \\
\end{align}\]
Now, we will write $\angle QSR=\angle OSQ+\angle OSR$ and substitute, \[\angle OSQ={{40}^{\circ }}\] from equation (7) and \[\angle OSR={{30}^{\circ }}\] from equation (8) in it. Then,
$\begin{align}
  & \angle QSR=\angle OSQ+\angle OSR \\
 & \Rightarrow \angle QSR={{40}^{\circ }}+{{30}^{\circ }} \\
 & \Rightarrow \angle QSR={{70}^{\circ }} \\
\end{align}$
Now, from the above result, we conclude that the measure of the $\angle QSR={{70}^{\circ }}$.

Note: Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer quickly. Moreover, though the question is very easy, we should apply the theorems and results related to the circles and triangles with full clarity so, that we can find the correct answer easily, and whenever we get stuck at some step we should refer the given figure always.