Question

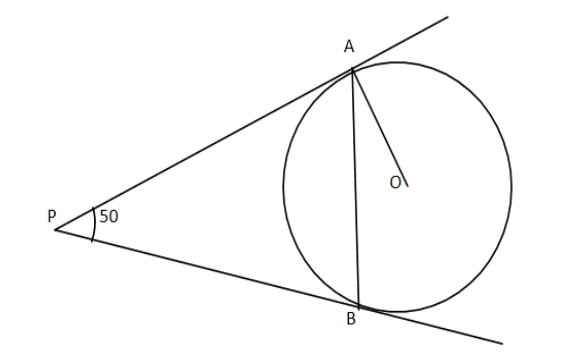
In the figure $PA,PB$ are the tangents to the circle with the centre $O$ such that $\angle APB = 90^\circ $, write the measure of $\angle OAB$

Answer 1

Hint:We know that the tangents drawn from the single point on the circle are equal and therefore $PA = PB$ and angle opposite to the equal sides are equal. So $\angle PAB = \angle PBA$. So we can calculate $\angle PAB$ in the triangle $PAB$ and we know that the tangent is always perpendicular to the line drawn from the centre to the point where tangent meets the circle. So $\angle PAO = 90^\circ $

Complete step-by-step answer:
Here in the above question, we are given that$PA,PB$ are the tangents to the circle with the centre $O$ such that$\angle APB = 90^\circ $. So let us draw the figure where $O$ is the centre. Now joining $OA,OB$ and we know that $OA = OB$ because both are equal to the radius.

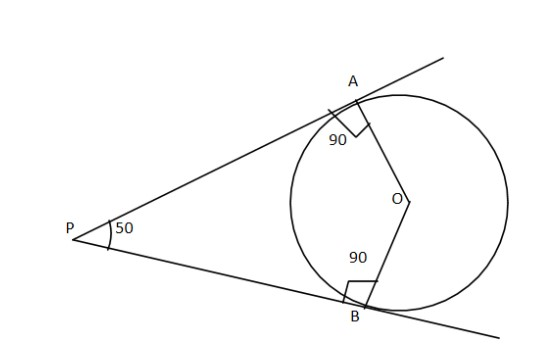
We also know that the tangent makes with the radius. So $\angle PAO = 90^\circ $ and $\angle PBO = 90^\circ $
Now joining $OP$, we get the two triangles $OPB,OPA$
And we know that $\angle OAP = \angle OBP$ as both are equal to $90^\circ $
Also we know that $OA = OB$ as both are equal to the radius of the circle and $OP = OP$ as both are common in the both triangles.
$\Delta OPB \cong \Delta OPA$ (By right hypotenuse side congruency)
So by the corresponding part of the congruent triangle, we say that $AP = BP$

Now again in $\Delta APB$ we proved that $AP = BP$ and we know that the angle opposite to the equal angles are equal.
$\angle BAP = \angle ABP - - - - - (1)$
Now we know that the sum of the angles in the triangle is equal to $180^\circ $
So $\angle BAP + \angle ABP + \angle APB = 180^\circ $
$\angle BAP + \angle BAP + 50^\circ = 180^\circ $as $\angle BAP = \angle ABP$.
$2\angle BAP = 130^\circ $
$\angle BAP = 65^\circ $
We also know that $\angle PAO = 90^\circ $
We can write it as
$\angle PAO = \angle PAB + \angle OAB$
So $\angle PAB + \angle OAB = 90$
$65^\circ + \angle OAB = 90^\circ $
$\angle OAB = 25^\circ $.

Note:From any external point we can draw two tangents to the circle and both are always equal and the tangent is always perpendicular to the radius joining the point of contact and distance from the centre to the circumference of the circle is always equal and is equal to the radius of the circle.Students should remember these definitions and properties of tangents drawn to circle for solving these types of questions.