Question

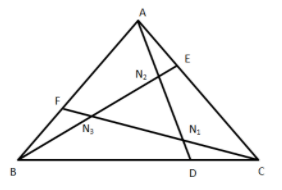
In the figure, $\overline {CD} $, $\overline {AE} $ and $\overline {BF} $ are one third of their respective sides. It follows that$\overline {A{N_2}} :\overline {{N_2}{N_1}} :\overline {{N_1}D} = 3:3:1$, and similarly for lines $BE$ and $CF$. Then the area of triangle ${N_1}{N_2}{N_3}$ is:

A) $\dfrac{1}{{10}}\vartriangle ABC$
B) $\dfrac{1}{9}\vartriangle ABC$
C) $\dfrac{1}{7}\vartriangle ABC$
D) $\dfrac{1}{6}\vartriangle ABC$

Answer 1

Hint:
Here, we are required to find the area of triangle ${N_1}{N_2}{N_3}$when $\overline {CD} $, $\overline {AE} $ and $\overline {BF} $ are one third of their respective sides and $\overline {A{N_2}} :\overline {{N_2}{N_1}} :\overline {{N_1}D} = 3:3:1$, and similarly for lines $BE$ and$CF$. We will draw the given figure again and label the ratios to their respective sides. After finding the relationship between each side with the help of ratios, we will find the area of $\vartriangle AB{N_2}$, $ar\vartriangle A{N_1}C$ and $ar\vartriangle B{N_3}C$. Subtracting these areas from the $\vartriangle ABC$ will give us the required area of $\vartriangle {N_1}{N_2}{N_3}$.

Complete step by step solution:
According to the question, it is given that,
 In the given figure, $\overline {CD} $, $\overline {AE} $ and $\overline {BF} $ are one third of their respective sides.
Since, $\overline {CD} $, $\overline {AE} $ and $\overline {BF} $ lies on the sides $BC$,$AC$ and $AB$ respectively.
Therefore, $CD = \dfrac{1}{3}BC$ or $3CD = BC$
Hence, we can say that 3 times $CD$ gives us $BC$.
Therefore, the ratio of $CD:BC = 1:2$as this will make the given condition true.
Similarly, $AE = \dfrac{1}{3}AC$
Hence, the ratio of $AE:AC = 1:2$
And, $BF = \dfrac{1}{3}AB$
Hence, the ratio of $BF:AB = 1:2$
Now, as we know,
Are of a triangle$ = \dfrac{1}{2} \times {\text{base}} \times {\text{height}}$
Since, $AE = \dfrac{1}{3}AC$
Hence, the base is one-third.
Therefore, Area of $\vartriangle ABE = \dfrac{1}{3}ar\vartriangle ABC$………………………………(1)
Also, according to the question, $\overline {A{N_2}} :\overline {{N_2}{N_1}} :\overline {{N_1}D} = 3:3:1$
And similarly for lines $BE$ and $CF$.

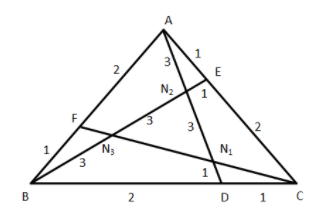
Now, $ar\vartriangle AB{N_2} = \dfrac{6}{7}ar\vartriangle ABE$……………………………………………..(2)
This is because the base of the $\vartriangle AB{N_2}$ i.e. $B{N_2}$ is $\dfrac{3}{7} + \dfrac{3}{7} = \dfrac{6}{7}$of the base of $\vartriangle ABE$ i.e. $BE$.
Therefore, from equation (1) and (2), we get,
$ar\vartriangle AB{N_2} = \dfrac{6}{7} \times \dfrac{1}{3}ar\vartriangle ABC$
$ \Rightarrow ar\vartriangle AB{N_2} = \dfrac{2}{7}ar\vartriangle ABC$
Similarly,
$ar\vartriangle BFC = \dfrac{1}{3}ar\vartriangle ABC$…………………………………..(3)
And, $ar\vartriangle B{N_3}C = \dfrac{6}{7}ar\vartriangle BFC$…………………………….(4)
Therefore, from the equations (3) and (4) , we get,
$ar\vartriangle B{N_3}C = \dfrac{6}{7} \times \dfrac{1}{3}ar\vartriangle ABC$
$ \Rightarrow ar\vartriangle B{N_3}C = \dfrac{2}{7}ar\vartriangle ABC$
And, again doing all the steps, we will get,
$ \Rightarrow ar\vartriangle A{N_1}C = \dfrac{2}{7}ar\vartriangle ABC$
Now, we are required to find the area of the triangle ${N_1}{N_2}{N_3}$.
If we observe the diagram carefully, then,
$ar\vartriangle {N_1}{N_2}{N_3} = ar\vartriangle ABC - ar\vartriangle AB{N_2} - ar\vartriangle B{N_3}C - ar\vartriangle A{N_1}C$
But, $ar\vartriangle AB{N_2} = ar\vartriangle A{N_1}C = ar\vartriangle B{N_3}C = \dfrac{2}{7}ar\vartriangle ABC$
Therefore, $ar\vartriangle {N_1}{N_2}{N_3} = ar\vartriangle ABC - 3ar\vartriangle AB{N_2}$
$ \Rightarrow ar\vartriangle {N_1}{N_2}{N_3} = ar\vartriangle ABC - 3\left( {\dfrac{2}{7}ar\vartriangle ABC} \right)$
$ \Rightarrow ar\vartriangle {N_1}{N_2}{N_3} = ar\vartriangle ABC - \dfrac{6}{7}ar\vartriangle ABC$
Taking LCM on RHS,
$ \Rightarrow ar\vartriangle {N_1}{N_2}{N_3} = \dfrac{{7 - 6}}{7}ar\vartriangle ABC = \dfrac{1}{7}ar\vartriangle ABC$
$\therefore ar\vartriangle {N_1}{N_2}{N_3} = \dfrac{1}{7}ar\vartriangle ABC$

Therefore, option C is the correct answer.

Note:
This question should be solved carefully as it required a high level of attention and observation. Drawing the figure carefully and labeling the ratios correctly as per the question is really important because if not labeled correctly then our answer would be completely wrong. Also, while using the formula of area of triangle, applying the ratios in the base (for instance, the base of the $\vartriangle AB{N_2}$ i.e. $B{N_2}$ is $\dfrac{3}{7} + \dfrac{3}{7} = \dfrac{6}{7}$of the base of $\vartriangle ABE$ i.e. $BE$.) helps us to find a relationship between two triangles and hence, reaching towards the desired answer.