Question

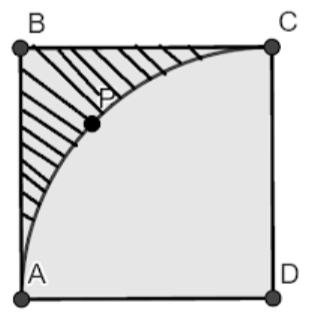
In the figure, OABC is a square of side 7cm. If OAPC is a quadrant of a circle with center O, then find the area of the shaded region. (Use\[\pi =\dfrac{22}{7}\])

Answer 1

Hint: OABC is a square. The area of a square is given by \[{{s}^{2}}\], where s is the length of all sides of a square. OAPC is a quadrant. Area of a quadrant is given by\[\dfrac{\theta }{360}\times \pi {{r}^{2}}\], where \[\theta \] is the angle of the sector and r is radius. We will find these two areas and subtract them to find the area of the shaded region.

Complete step-by-step solution:
It is given that OABC is a square with side 7cm.
\[\Rightarrow OA=7cm\]
Area of a square with side sis given by \[{{s}^{2}}\].
\[\therefore ar(\square OABC)={{(7)}^{2}}=49c{{m}^{2}}---(1)\]
It is also given that OAPC is a quadrant of a circle with center O.
This implies that OA is the radius. We know that the quadrant of the circle makes \[{{90}^{\circ }}\] with the circle.
Therefore, OA=r=7cm
\[\angle COA={{90}^{\circ }}\]
We know that the area of a sector with angle \[\theta \] and radius r is given by, \[\dfrac{\theta }{360}\times \pi {{r}^{2}}\]
\[\therefore \] Area of OAPC \[\begin{align}
  & =\dfrac{90}{360}\times \dfrac{22}{7}\times {{(7)}^{2}} \\
 & =38.5c{{m}^{2}}----(2) \\
\end{align}\]
Now, area of shaded region.
= Area of square OABC-area of quadrant OAPC
From equation (1) and (2), we get,
Area of shaded region \[\begin{align}
  & =(44-38.5)c{{m}^{2}} \\
 & =10.5c{{m}^{2}} \\
\end{align}\]
Hence, the required answer is \[10.5c{{m}^{2}}\]

Note: We know 4 quadrants make a circle. This means that,
\[4\times \] Area of 1 quadrant=area of circle
\[\Rightarrow \] Area of a quadrant = \[\dfrac{1}{4}\times \] area of circle
= \[\dfrac{1}{4}(\pi {{r}^{2}})\]
Where r is the radius of the circle.
This formula can always be directly put whenever dealing with quadrants.
The best way to approach the questions involving the area of the shaded region is to identify all the plane figures that result in the shaded regions. Once we know all the plane figures, we will find their areas and add or subtract them accordingly to find the area of the shaded region. Also the question mentioned to use the value of \[\pi =\dfrac{22}{7}\]. Using any other value would result in an approximate answer but not the exact one. This may lead to a deduction in scoring. So, we should read the question thoroughly and then solve the question.