Question

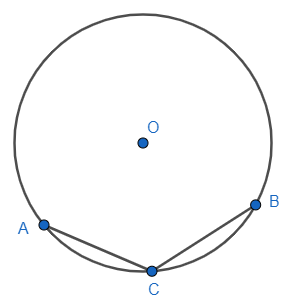
In the figure, O is the centre of the circle and ACB is a minor arc, then $\angle ACB$ is

a) Obtuse
b) Acute
c) Right
d) Reflex

Answer 1

Hint: Join AO, OC, OB radii in the given circle. Take angle AOC and BOC as two different variables and try to get angle OCB and angle OAC with the help of property of a triangle that sum of angles in a triangle is ${{180}^{\circ }}$ and angles opposite to equal sides in a triangle are equal. Get angle ACB by adding $\angle OCA,\angle OCB$ . Use the definition of minor arc and major arc in the circle, that are given as
Minor arc: Angle at centre by minor arc is less than ${{90}^{\circ }}$ .
Major arc: Angle at centre by major arc is greater than ${{90}^{\circ }}$ and lower than ${{180}^{\circ }}$.

Complete step-by-step answer:
For solving the given problem, let us first try to understand the concept of minor and major arcs in a circle. Arcs of a circle are defined on the basis of angles formed by them at centre, which is also termed as central angle. A minor arc is less than ${{180}^{\circ }}$ at the centre whereas a major arc is greater than ${{180}^{\circ }}$ .

Where $\theta =\text{ Centre angle}$
Now, coming to the question, the diagram in the problem is given as

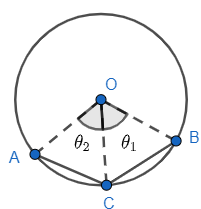
Let us join O and A, O and C, O and B and all the lengths OA, OB, OC will be equal as they are representing the radii of the given circle. Now, suppose
$\angle BOC={\theta_1},\angle AOC={\theta_2}$
As we know angles in a triangle are equal to each other. So, in $\Delta BOC$ sides OB and OC are equal to each other, so $\angle OBC,\angle BCO$ should be equal. So, we get
$\angle OBC=\angle BCO..................\left( i \right)$
We know sum of angles of a triangle is ${{180}^{\circ }}$ it means
$\begin{align}
  & \angle BOC+\angle OBC+\angle BCO={{180}^{\circ }} \\
 & {{\theta }_{1}}+\angle OBC+\angle BCO={{180}^{\circ }} \\
\end{align}$
As, angles OBC and BCO are equal, so we get
$\begin{align}
  & \theta +2\angle BCO=180 \\
 & \angle BCO=\dfrac{180-{{\theta }_{1}}}{2} \\
 & \angle BCO=90-\dfrac{{{\theta }_{1}}}{2}..........................\left( ii \right) \\
\end{align}$
Similarly in triangle AOC, we have
$\begin{align}
  & \angle AOC+\angle OCA+\angle ACO={{180}^{\circ }} \\
 & {{\theta }_{2}}+\angle OCA+\angle ACO={{180}^{\circ }} \\
\end{align}$
As, $\angle OCA=\angle ACO$ , because OA = OC in this triangle as well. So, we get
$\begin{align}
  & {{\theta }_{2}}+2\angle OCA={{180}^{\circ }} \\
 & \angle OCA=\dfrac{180-{{\theta }_{2}}}{2} \\
 & \angle OCA=90-\dfrac{{{\theta }_{2}}}{2}.........................\left( iii \right) \\
\end{align}$
Now, we can write angle ACB as the sum of angles OCA and OCB. So, we get
$\angle ACB=\angle OCA+\angle BCO$
From equation (ii) and (iii) we can put values of angles OCA and BCO in the above equation. Hence, we get
$\begin{align}
  & \angle ACB=90-\dfrac{{{\theta }_{1}}}{2}+90-\dfrac{{{\theta }_{2}}}{2} \\
 & \angle ACB=180-\dfrac{1}{2}\left( {{\theta }_{1}}+{{\theta }_{2}} \right) \\
\end{align}$
Now, as ${{\theta }_{1}},{{\theta }_{2}}$ are the angles in the minor arc so, both should be acute angles. Hence the sum of them can only be ${{180}^{\circ }}$ as maximum. So, we can write inequality as
$O<{{\theta }_{1}}+{{\theta }_{2}}<180$
Dividing the whole equation by 2 we get
$\begin{align}
  & O<\dfrac{{{\theta }_{1}}+{{\theta }_{2}}}{2}<\dfrac{180}{2} \\
 & O<\dfrac{{{\theta }_{1}}+{{\theta }_{2}}}{2}<90 \\
\end{align}$
Hence angle ACB can get maximum at the minimum value of
$\dfrac{{{\theta }_{1}}+{{\theta }_{2}}}{2}$
So, angle ACB will be maximum as ${{180}^{\circ }}$ . Similarly angle ACB be minimized by putting the maximum value of
$\dfrac{{{\theta }_{1}}+{{\theta }_{2}}}{2}$
So, it can only be ${{90}^{\circ }}$ at maximum for ${{\theta }_{1}}+{{\theta }_{2}}={{180}^{\circ }}$ . Hence angle ACB will get ${{90}^{\circ }}$ as minimum value. So, we get
${{90}^{\circ }}<\angle ACB<{{180}^{\circ }}$
Now, we know the angles greater than ${{90}^{\circ }}$ and lower than ${{180}^{\circ }}$ are termed as obtuse angles
Hence, option (a) is correct.

Note: Another approach for observing the angle ACB would be that we need to draw lots of chord making angle to C, which can be observed as

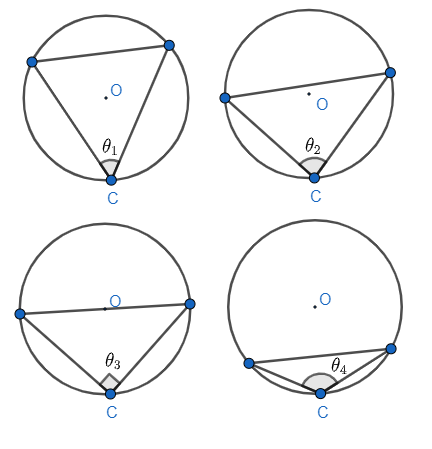
Where, we can observe that
$\begin{align}
  & {{\theta }_{1}}<{{\theta }_{2}}<{{\theta }_{3}}<{{\theta }_{4}} \\
 & \Rightarrow {{\theta }_{3}}={{90}^{\circ }}\left( \text{Angle in semi-circle} \right) \\
\end{align}$
It means the angle given in the problem will be greater than ${{90}^{\circ }}$ as per the relation of above inequality. So, it can be another approach as well.
Terms need to be clear in the given options. One may go wrong with the terminology point of view as well. Terms in option are defined as
Obtuse: Angle between ${{90}^{\circ }},{{180}^{\circ }}$
Right: ${{90}^{\circ }}$ angle
Reflex: Angle between ${{180}^{\circ }},{{360}^{\circ }}$