Question

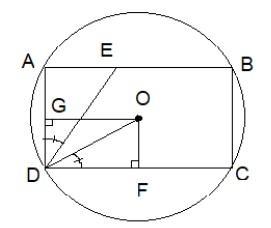
In the figure (not drawn to scale), rectangle ABCD is inscribed in the circle with the Centre at O. The length of side AB is greater than that of side BC. The ratio of the area of circle to the area of rectangle is $\pi :\sqrt 3 $ . The line segment DE interests AB at E such that $\angle ODC = \angle ADE$ what is the ratio of $AE:AD$ ?

A. $\dfrac{1}{{\sqrt 3 }}$
B. $\dfrac{1}{{\sqrt 2 }}$
C. $\dfrac{1}{{2\sqrt 3 }}$
D. $\dfrac{1}{2}$

Answer 1

Hint:Using the property of a rectangle inscribed in a circle i.e. perpendicular from the center of circle bisect the side of the rectangle. We will use basic trigonometric relations to solve the problem.

Complete step-by-step answer:
Let the angle $\angle ADE = \angle ODF = \theta $
Draw a perpendicular OF from O to side DC and OG from O to side AD
According to property of circle, when a rectangle is inscribed in a circle then the perpendicular from the center of circle to sides of the rectangle bisects them.
Hence DF = FC and AG = GD
Now in $\vartriangle ODF$
$
  \dfrac{{OF}}{{OD}} = \sin \theta \\
    \\
 $
$\therefore OF = OD\sin \theta $
And $\dfrac{{DF}}{{OD}} = \cos \theta $
$\therefore DF = OD\cos \theta $
Since AB = CD (opposite sides of rectangle are equal)
$CD = 2DF$
$\therefore CD = OD\cos \theta $ (from above)
Now, OFDG is also a rectangle since it is a parallelogram with all right angles and an unequal adjacent side.
Hence, $AD = BC = 2OF = 2OD\sin \theta $
Now given,
Area of circle: Area of rectangle = $\pi :\sqrt 3 $
Hence $\dfrac{{\pi {{(OD)}^2}}}{{AB*AD}} = \dfrac{\pi }{{\sqrt 3 }}$
On canceling $\pi $ from both side and cross multiplying we get,
 $AB*AD = {(OD)^2}\sqrt 3 $
Now using above relations, we get
$2(OD)\cos \theta *2(OD)\sin \theta = \sqrt 3 {(OD)^2}$
$\because 2\sin \theta \cos \theta = \sin 2\theta $ (Trigonometric identity)
Using these equations, we get
$
  \therefore 2{(OD)^2}\sin 2\theta = \sqrt 3 {(OD)^2} \\
  \sin 2\theta = \dfrac{{\sqrt 3 }}{2} \\
  2\theta = {\sin ^{ - 1}}(\dfrac{{\sqrt 3 }}{2}) \\
  \therefore 2\theta = \dfrac{\pi }{3} \\
  \theta = \dfrac{\pi }{6} \\
 $
Now in $\vartriangle ADE$
$
  \dfrac{{AE}}{{AD}} = \tan \theta \\
  \because \theta = \dfrac{\pi }{6} \\
  \therefore \tan \dfrac{\pi }{6} = \dfrac{1}{
  \sqrt 3 \\
    \\
 } \\
 $

So, the correct answer is “Option A”.

Note: In a rectangle inscribed in a circle the diagonal of the rectangle is the diameter of the circle. The Centre of circle is the intersection point of diagonals. Analysis of figures is very important in geometry, once analysis is done your half work is done.