Question

In the figure given below, \[\angle BED=\angle BDE\] and E is the middle point of BC. Prove that \[\dfrac{AF}{CF}=\dfrac{AD}{BE}\]

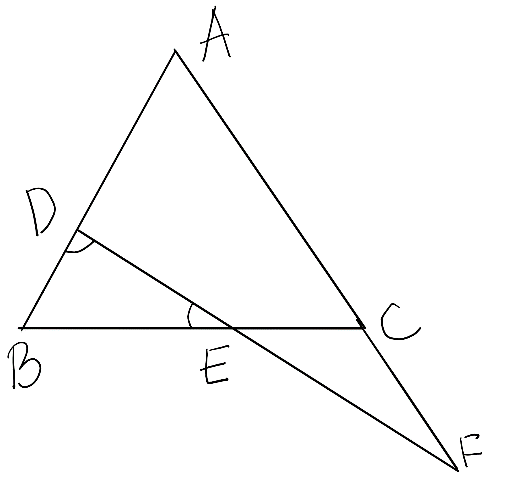
Answer 1

Hint: To solve this question and prove what is needed, we will first of all assume that, \[\angle BED=\angle BDE\] is \[{{x}^{o}}\]. Now we will use the fact that E is the middle point of BC that means BE=EC. Now lastly we will use that \[\Delta BED\] and \[\Delta CEG\] are similar, which will give the required result.

Complete step by step solution:
Given that in the figure, \[\angle BED=\angle BDE\] and E is the middle point of BC.
We have to prove that \[\dfrac{AF}{CF}=\dfrac{AD}{BE}\].

As the figure represents, \[\angle BED=\angle BDE\] and we have to prove that \[\dfrac{AF}{CF}=\dfrac{AD}{BE}\], that is, the ratio of the four sides are equal to each other.
We will assume that, \[\angle BED=\angle BDE\] is \[{{x}^{o}}\].
Hence the \[\Delta BDE\], as E is the midpoint of the line BC, we have,
 \[BD\text{ }=\text{ }BE\text{ }=\text{ }\dfrac{BC}{2}\]
Now we have to draw a line CG in parallel to AB in the triangle.
This can be shown as,

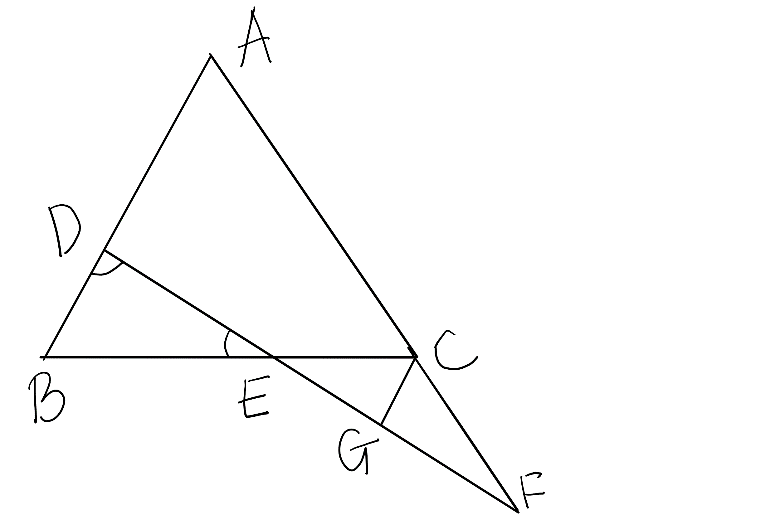
Let \[\angle CEG\] be = \[{{x}^{o}}\] (vertical angle).
Now, \[\Delta BED\] and \[\Delta CEG\] are similar as they have the parallel lines given as,
CE || BE, CG || BD, EG || ED.
Hence \[\angle CEG~=\angle CGE\text{ }=~{{x}^{o}}\] and \[\angle ECG\text{ }=\angle B\].
Now for the \[\Delta ABC\], \[\angle FCB\] is an external angle.
 \[\Rightarrow ~\angle FCB\text{ }=\angle A+\angle B\]
Hence, \[\angle GCF\text{ }=~\angle A\].
Further, as EGF is a line gives,
\[\angle CGF=180{}^\circ -~\angle CGE=180{}^\circ -~x\]
In \[\Delta CGF,~\angle F\text{ }=180{}^\circ -~\angle A-\left( 180{}^\circ -x{}^\circ \right)=\text{ }x{}^\circ -\angle A\]
Now compare \[\Delta ADF\] and \[\Delta CGF\].
We see that all the angles of both the triangles are the same.
Since all corresponding angles are the same, they are similar triangles.

\[\Rightarrow \]\[\dfrac{AF}{AD}=\dfrac{CF}{CG}=\dfrac{CF}{CE}=\dfrac{CF}{BE}\]
\[\Rightarrow \]\[\dfrac{AF}{CF}=\dfrac{AD}{BE}\]
Hence the above equation is proved.
Therefore, we are done proving the required.


Note: The possibility of error in these types of questions can be at the point where students have to choose which property to apply while using the fact of similar triangles. For this, categorize which all angles or sides we need in the triangle and then use only them to get the result. This makes the question easier to solve.