Question

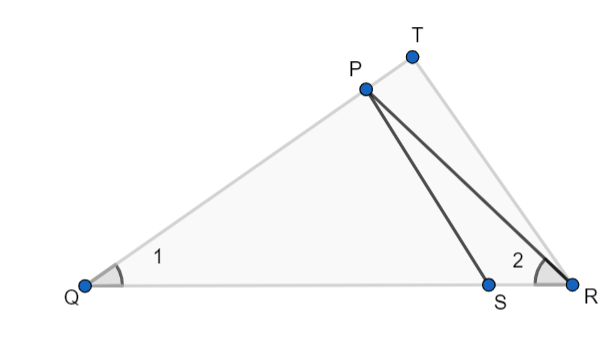
In the figure, $\dfrac{QR}{QS}=\dfrac{QT}{PR}$ and $\angle 1=\angle 2$ . Show that $\vartriangle PQS\sim \vartriangle TQR$

Answer 1

Hint: To solve this question, we will use the property of a triangle which is sides opposite to two equal angles sides are the same, then sides are also equal. Using, this property in triangle $\vartriangle PQR$, we will modify $\dfrac{QR}{QS}=\dfrac{QT}{PR}$ for triangles $\vartriangle PQS$ and $\vartriangle TQR$. And using this, we will prove that $\vartriangle PQS\sim \vartriangle TQR$.

Complete step by step answer:

Before we solve the question, let us see what does $\sim $means in triangles and what some important properties of triangles are.
In triangles, if two triangles are similar then the similarity is denoted by $\sim $. The similarity of two triangles means they have the same angle measures and have a length of sides in ratio.
Some of the properties of the triangle are:
( a ) Angle opposite to two equal sides are the same, then angles is also equal. Vice versa is also true of this statement.
( b ) Interior angle sum of triangle is equals to ${{180}^{{}^\circ }}$ .
( c ) Area of triangle is $\dfrac{1}{2}\times b\times h$ , where b is the base of the triangle and h is the height of the triangle.

Now, in question it is given that $\angle 1=\angle 2$, so we discussed that sides opposite to two equal angles sides are the same, then sides are also equal.
So, in triangle $\vartriangle PQR$, we can say that
PQ = PR
Now, it is given that $\dfrac{QR}{QS}=\dfrac{QT}{PR}$
As we know that PQ = PR, so we can also say that
$\dfrac{QR}{QS}=\dfrac{QT}{QP}$……. ( i )
In triangle $\vartriangle PQR$ and $\vartriangle TQR$, by equation ( i )
$\dfrac{QP}{QT}=\dfrac{QS}{QR}$….. ( ii )
From figure, we can see that using ( ii ), that QP is proportional to QT and QS is proportional to QR and QP and QS are sides of triangle $\vartriangle PQS$ and QT and QR are sides of triangle $\vartriangle TQR$ also, $\angle Q$ is the common angle for both triangles.
Hence, using SAS(side-angle-side) similarity criterion, We can say that
$\vartriangle PQS\sim \vartriangle TQR$

Note:
To solve such a question, one must know the properties of the triangle which really helps in solving questions based on the similarity of triangles. Try to dig all the hints in question and use them in solving in question. Take the help of a figure to solve questions more easily.