Question

In the figure below, the rectangle at the corner measures $ 10cm\times 20cm $ . The corner A of the rectangle is also a point on the circumference of the circle. What is the radius of the circle in cm?

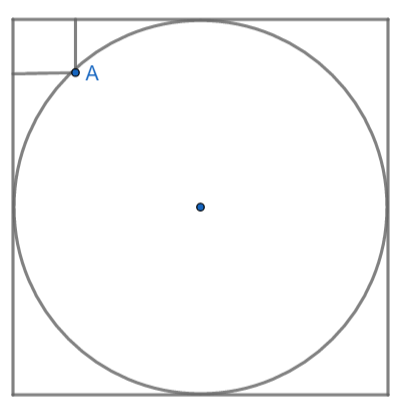
\[\begin{align}
  & A.10cm \\
 & B.40cm \\
 & C.50cm \\
 & D.30cm \\
\end{align}\]

Answer 1

Hint: For solving this sum, we will first suppose the radius of the circle as 'r'. After that, we will draw the radius of circles such that we have a right-angled triangle with our vertex aa the center of the circle and another vertex as A. Using the figure we will use Pythagoras theorem in the right-angled triangle and calculate the value of r.

Complete step by step answer:
Here we are given the figure of a circle and rectangle. Let us connect center O of the circle to point A. Then let us draw a radius OB of the circle parallel to the breadth of the rectangle. After that, let us join A to the radius OB at point C such that AC is perpendicular to OB. Let us draw radius OD parallel to the length of the rectangle. Our figure looks like this,

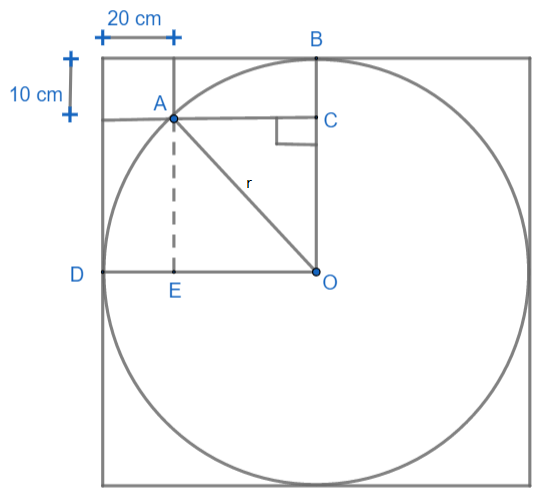
Here we have supposed the radius of the circle as r, therefore OA = r, OB = r, OD = r.
We can see from the figure that, triangle OAC is a right angled triangle. Now, we have OA = r, OB can be written as OC + CB.
As CB is parallel and equal to breadth of rectangle (10cm) then, BC = 10cm, so we have r = OC + 10cm. Therefore, OC = (r-10)cm.
Now OD = r and OD = OE + ED, we can see that ED = 20cm, so r = OE + 20cm, OE = (r-20)cm.
Also, we can see that AC = EO, therefore, AC is equal to (r-20)cm.
In $ \Delta AOC $ we have AO = r cm, OC = (r-10)cm and AC = (r-20)cm.
By applying Pythagoras theorem, $ {{\left( \text{hypotenuse} \right)}^{2}}={{\left( \text{base} \right)}^{2}}+{{\left( \text{perpendicular} \right)}^{2}} $ .
We have, \[{{\left( \text{AO} \right)}^{2}}={{\left( \text{OC} \right)}^{2}}+{{\left( \text{AC} \right)}^{2}}\Rightarrow {{r}^{2}}={{\left( r-10 \right)}^{2}}+{{\left( r-20 \right)}^{2}}\].
Using $ {{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab $ we get $ {{r}^{2}}={{r}^{2}}{{\left( 10 \right)}^{2}}-2\left( 10 \right)\left( r \right)+{{r}^{2}}+{{\left( 20 \right)}^{2}}-2\left( 20 \right)\left( r \right) $ .
Simplifying we get
\[\begin{align}
  & {{r}^{2}}=2{{r}^{2}}+100-20r+400-40r \\
 & \Rightarrow -{{r}^{2}}=500-60r \\
 & \Rightarrow {{r}^{2}}-60r+500=0 \\
\end{align}\]
We know $ -50\times -10=500\text{ and }-50-10=-60 $ .
So splitting the middle term we get,
\[\begin{align}
  & {{r}^{2}}-50r-10r+500=0 \\
 & \Rightarrow r\left( r-50 \right)-10\left( r-50 \right)=0 \\
 & \Rightarrow \left( r-10 \right)\left( r-50 \right)=0 \\
\end{align}\]
Putting both factors equal to zero we get,
 $ r-10=0\text{ and }r-50=0\Rightarrow r=10\text{ and }r=50 $ .
As we can see r cannot be 10cm therefore, r = 50cm.
Hence option C is the correct answer.

Note:
Students should note that we have drawn AE perpendicular to OD and AC and thus we have rectangle ACEO, so AC = EO. They should note that r cannot be equal to 10cm because if r = 10cm then OC = 0 cm which is not possible. Take care of signs while splitting the middle term.