Question

In the figure, BC is the diameter. What is the measure of x?

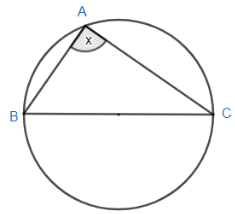
Answer 1

Hint: First draw the diameter of a circle. Mark the endpoints as BC. Take any point A on the circle. Now, join the A, B, C to form a triangle. Now mark the center of the circle as O. Take the line segments OA, OB, OC. Now use the concept of sine rule to find the angles at vertices. Then take that sum of all interior angles is ${{180}^{\circ }}$. Sine rule is given by:
$\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}=2R$ .
Complete step-by-step solution -
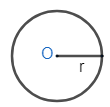
First, draw a circle with center O and radius r.

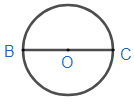
Now draw the diameter of the given circle and mark the endpoints as B, C.

Take a random point A on the circle and from triangle:

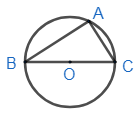
Now mark the radius of all points as ‘r’, we get:

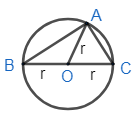
Now, apply sine rule to triangle OAB, we get it as:
$\dfrac{\sin \left( OBA \right)}{r}=\dfrac{\sin \left( OAB \right)}{r}$
By cancelling common terms we get relation of angles as:
$OBA=OAB$
Let us assume these angles as variable a, so, we get:
$OBA=OAB=a$
Now, apply sine rule to triangle OAC, we get it as:
$\dfrac{\sin \left( OAC \right)}{r}=\dfrac{\sin \left( OCA \right)}{r}$
By cancelling the common terms, we get the relation of angles as:
$OAC=OCA$
Now assume these angles as variable b. So, we get:
$OAC=OCA=b$
Now take the sum of angles of a triangle will be 180:
$OBA+BAC+OCA=180$ from triangle ABC.
We can break angle BAC into 2 parts: $BAC=OAC+OAB$
By substituting this equation, we get the relation as:
$OBA+OAB+OAC+OCA=180$
By substituting their values back into the equation we get:
$2\left( a+b \right)=180$
By dividing with 2 on both sides, we get value as: $a+b=90$
As per given question we have $a+b=BAC$ .
Given in the question that $BAC=x$. So, by this, we get the value of x to be given by $x={{90}^{\circ }}$.
Therefore the measure of x in the given figure is ${{90}^{\circ }}$.

Note: Be careful while drawing diagrams as we need them the whole way through. An alternate method is doubling them. The angle at any part is the angle subtended by it at center divided by 2. So, here at O the point A subtends ${{180}^{\circ }}$ because BC is a diameter. So, we get the same result in any method.