Question

In The figure, AHKF, FKDE and HBCK are unit squares: AD and BF intersect in X. Then the ratio of the areas of the triangles AXF and ABF is?

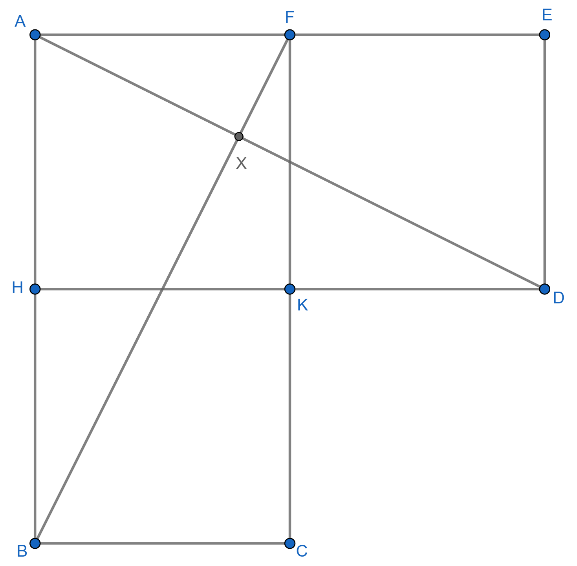
(a) $\dfrac{1}{4}$
(b) $\dfrac{1}{5}$
(c) $\dfrac{1}{6}$
(d) $\dfrac{1}{8}$

Answer 1

Hint: For solving this question first we will draw a segment XP perpendicular to AF. After that, we will see the result of the Basic Proportionality theorem and we will use it to find the length of the height XP for the triangle AXF. Then, we will calculate the area of triangles AXF and ABF separately with the formula of $\dfrac{1}{2}\left( base \right)\left( height \right)$ and then find their ratio.

Complete step-by-step answer:
Given:
We have the following figure and we have to find the ratio of areas of the triangles AXF and ABF.

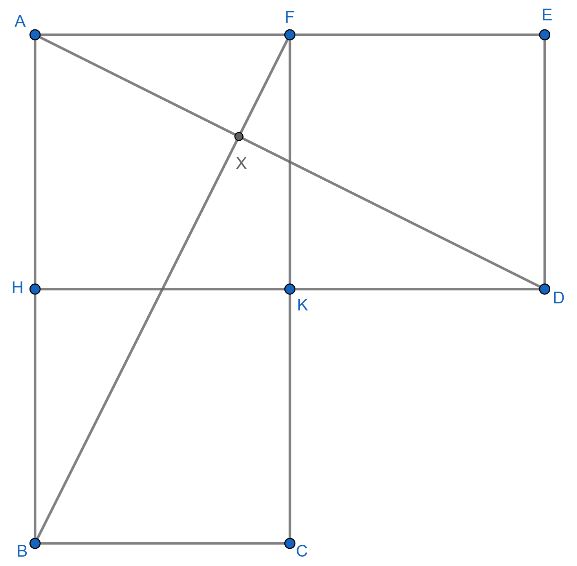
And it is given that AHKF, FKDE and HBCK are unit squares which means the length of their sides will be 1 unit.
Now, we draw the given figure with some extra construction. Look at the figure given below:

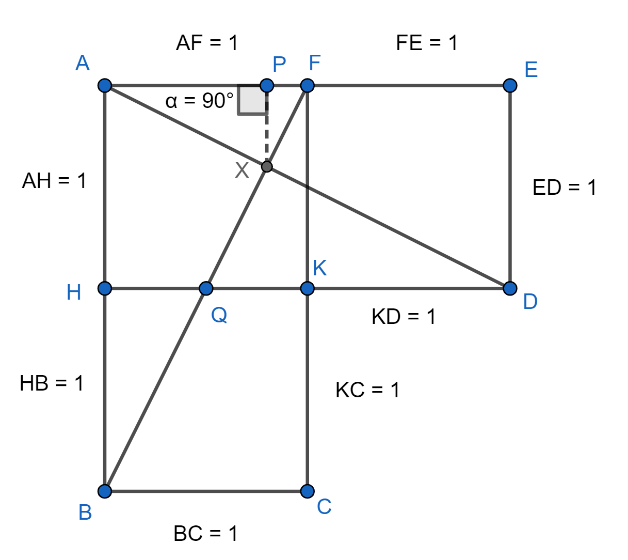
In the above figure, we have constructed an XP segment, which is parallel to FK, ED and perpendicular to the side AF.
Now, before we proceed we should know an important theorem which is called Basic Proportionality theorem.
Basic Proportionality Theorem $\left( BPT \right)$ :
Consider a $\Delta ABC$ and a line PQ parallel to the side BC intersects side AB at Q and side AC at P. For more clarity look the figure given below:

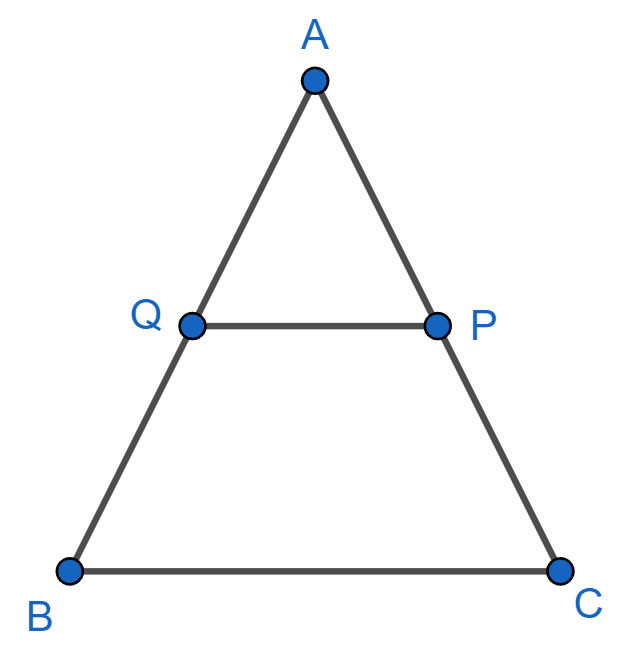
Now, as PQ is parallel to the side BC so, $\angle AQP=\angle ABC$ and $\angle APQ=\angle ACB$ as they are corresponding angles.
Now, consider $\Delta ABC$ and $\Delta AQP$ . Then,
$\begin{align}
  & \angle BAC=\angle QAP\text{ }\left( common \right) \\
 & \angle AQP=\angle ABC\text{ }\left( corresponding\text{ }angles \right) \\
 & \angle APQ=\angle ACB\text{ }\left( corresponding\text{ }angles \right) \\
\end{align}$
Now, as all the angles of the triangles are equal, so $\Delta ABC\sim \Delta AQP$ . And we know that for every similar triangles ratio of the corresponding sides is equal. Then,
$\dfrac{AB}{AQ}=\dfrac{AC}{AP}=\dfrac{QP}{BC}$
Now, from the Basic Proportionality theorem, we say that if PQ is drawn parallel to the side BC and it intersects side AB at Q and side AC at P. Then,
$\dfrac{AB}{AQ}=\dfrac{AC}{AP}=\dfrac{QP}{BC}$
Now, we come back to our problem in which we have the following figure:

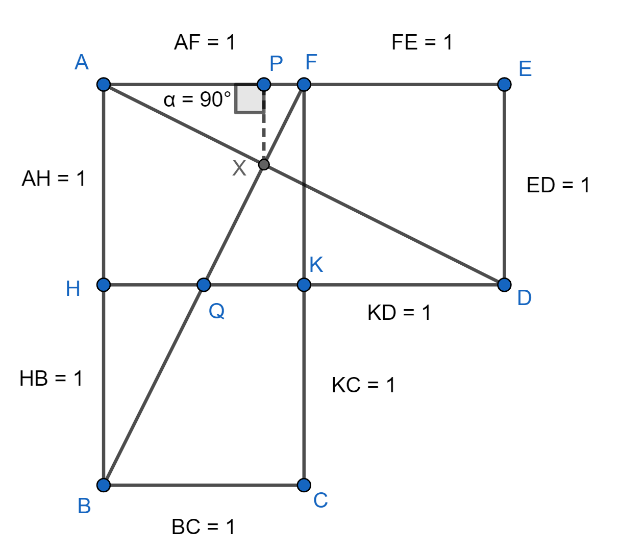
Now, first, consider $\Delta BFC$ in which BC is of 1 unit and FC is of 2 units. We can say that QK is parallel to the side BC and K is the midpoint of the side FK. Then,
$\begin{align}
  & \dfrac{QK}{BC}=\dfrac{FK}{FC}\text{ }(BPT) \\
 & \Rightarrow \dfrac{QK}{1}=\dfrac{1}{2} \\
 & \Rightarrow QK=0.5 \\
\end{align}$
Now, as we know that DK is of 1 unit and $DQ=DK+QK$ . Then,
$\begin{align}
  & DQ=1+0.5 \\
 & \Rightarrow DQ=1.5.............\left( 1 \right) \\
\end{align}$
Now, consider $\Delta AXF$ and $\Delta DXQ$ . Then,
$\begin{align}
  & \angle AXF=\angle DXQ\text{ }\left( vertically\text{ }opposite\text{ }angles \right) \\
 & \angle XAF=\angle XDQ\text{ }\left( alternate\text{ int}erior\text{ }angles \right) \\
 & \angle XFA=\angle XQD\text{ }\left( alternate\text{ int}erior\text{ }angles \right) \\
\end{align}$
Now, as all the angles of the triangles are equal, so $\Delta AXF\sim \Delta DXQ$ . And we know that for every similar triangles ratio of the corresponding sides is equal. Then,
$\dfrac{AX}{DX}=\dfrac{AF}{DQ}$
Now, put $DQ=1.5$ from equation (1), $DX=AD-AX$ and it is given that $AF=1$ . Then,
$\begin{align}
  & \dfrac{AX}{DX}=\dfrac{AF}{DQ} \\
 & \Rightarrow \dfrac{AX}{AD-AX}=\dfrac{1}{1.5} \\
 & \Rightarrow 1.5AX=AD-AX \\
 & \Rightarrow 2.5AX=AD \\
 & \Rightarrow \dfrac{AX}{AD}=\dfrac{2}{5}..................\left( 2 \right) \\
\end{align}$
Now, consider $\Delta ADE$ in which DE is 1 unit. We can say that XP is parallel to the side DE. Then,
$\dfrac{XP}{DE}=\dfrac{AX}{AD}$
Now, put $\dfrac{AX}{AD}=\dfrac{2}{5}$ from equation (2). Then,
$\begin{align}
  & \dfrac{XP}{DE}=\dfrac{AX}{AD} \\
 & \Rightarrow \dfrac{XP}{1}=\dfrac{2}{5} \\
 & \Rightarrow XP=0.4....................\left( 3 \right) \\
\end{align}$
Now, for $\Delta ABF$ the length of base AF is equal to 1 unit and height AB is of 2 units. Then,
$\begin{align}
  & Are{{a}_{\Delta ABF}}=\dfrac{1}{2}\left( base \right)\left( height \right) \\
 & \Rightarrow Are{{a}_{\Delta ABF}}=\dfrac{1}{2}\times 1\times 2 \\
 & \Rightarrow Are{{a}_{\Delta ABF}}=1....................\left( 4 \right) \\
\end{align}$
Now, for $\Delta AXF$ the length of base AF is equal to 1 unit and height XP is of 0.4 unit from equation (3). Then,
$\begin{align}
  & Are{{a}_{\Delta AXF}}=\dfrac{1}{2}\left( base \right)\left( height \right) \\
 & \Rightarrow Are{{a}_{\Delta AXF}}=\dfrac{1}{2}\times 1\times 0.4 \\
 & \Rightarrow Are{{a}_{\Delta AXF}}=0.2....................\left( 5 \right) \\
\end{align}$
Now, from the equation (4) and (5) calculate the ratio of the area of the triangles AXF and ABF. Then,
$\begin{align}
  & \dfrac{Are{{a}_{\Delta AXF}}}{Are{{a}_{\Delta ABF}}}=\dfrac{0.2}{1} \\
 & \Rightarrow \dfrac{Are{{a}_{\Delta AXF}}}{Are{{a}_{\Delta ABF}}}=\dfrac{1}{5} \\
\end{align}$
Now, from the above result, we conclude that the required ratio is $\dfrac{1}{5}$ .
Hence, (b) is the correct option.

Note: Here, the student should first understand what is asked in the question and then proceed in the right direction to get the correct answer quickly. After that, we should not be confused while applying the result of the Basic proportionality theorem and we should proceed stepwise to avoid confusion. Moreover, while solving such questions, we should always refer to the diagram if we get stuck at some step and try to figure out the best way to solve it.