Question

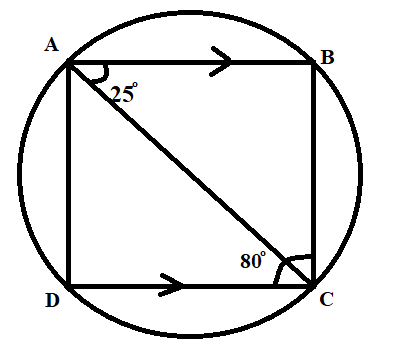
In the figure, AB is parallel to DC, \[\angle BCD={{80}^{\circ }}\text{ and }\angle BAC={{25}^{\circ }}.\] Then $\angle CAD$ is

(a) $55{}^\circ $
(b) $65{}^\circ $
(c) $75{}^\circ $
(d) $35{}^\circ $

Answer 1

Hint: For solving this question, we proceed from the given part that AB is parallel to DC. By using alternate angles property, $\angle ACD$ is equal to\[\angle BAC\]. Also, by using straight line property $\angle BCE$ and thus $\angle CBA$ is evaluated. Now, we take triangle ABC and by using the sum of all the angles in the triangle is 180 in degrees, we evaluate $\angle BAC$. The sum of the $\angle DAB\text{ and }\angle \text{DCB}$ is equal to 180 degree because “the opposite angles of cyclic quadrilateral are supplementary”. By using this theorem, we get $\angle CAD$.

Complete step-by-step answer:
Construction: Draw an external point E on produced DC

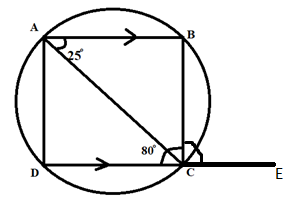
As per given in the question, AB is parallel to DC. So,
$\angle ACD=\angle BAC=25{}^\circ $ (Using alternate angles property)
Now, line DE is straight line. So, the angle sum of both angles is 180 degrees.
\[\begin{align}
  & \angle BCD+\angle BCE=180{}^\circ \\
 & 80{}^\circ ++\angle BCE=180{}^\circ \\
 & \angle BCE=\left( 180-80 \right){}^\circ \\
 & \angle BCE=100{}^\circ \\
\end{align}\]
$\angle ABC=\angle BCE=100{}^\circ $ (Using alternate angles property considering an external point E produced on DC)
Now, we take triangle ABC and apply the angle sum property i.e. “The sum of all angles in the triangle are ${{180}^{\circ }}$”.
In $\Delta ABC$
$\angle CAB+\angle ABC+\angle BCA={{180}^{\circ }}$ (By angle sum property)
$\begin{align}
  & \Rightarrow 25{}^\circ +100{}^\circ +\angle BCA=180{}^\circ \\
 & \Rightarrow 125{}^\circ +\angle BCA=180{}^\circ \\
 & \Rightarrow \angle BCA=180{}^\circ -125{}^\circ \\
 & \Rightarrow \angle BCA=55{}^\circ \\
\end{align}$
The angle BCA is $55{}^\circ $.
Now, the sum of angles DCB and DAB are ${{180}^{\circ }}$, by using the theorem “the opposite angles of cyclic quadrilateral are supplementary”. Therefore,
$\angle DAB+\angle DCB=180{}^\circ $
Here, $\angle DAB$ is the sum of the angle’s CAD and CAB. Similarly, $\angle DCB$ is the sum of the angles ACD and BCA. So, it can be mathematically expressed as:
$\begin{align}
  & \Rightarrow \left( \angle CAD+\angle CAB \right)+\left( \angle ACD+\angle BCA \right)=180{}^\circ \\
 & \Rightarrow \left( \angle CAD+25{}^\circ \right)+\left( 25{}^\circ +55{}^\circ \right)=180{}^\circ \\
 & \Rightarrow \angle CAD=180{}^\circ -105{}^\circ \\
 & \Rightarrow \angle CAD=75{}^\circ \\
\end{align}$
Hence, the angle CAD is $75{}^\circ $.
Hence, option (c) is correct.

Note: The key step for solving this problem is the consideration of an external point E on the produced DC to evaluate the value of angle BCA. Properties of the cyclic quadrilateral are essential and hence must be remembered.