Question

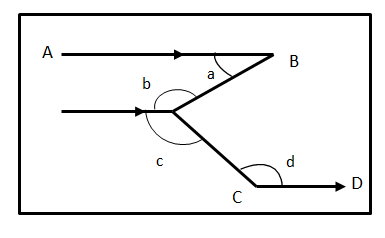
In the figure, AB is parallel to CD, which of the following statements is true?

A.\[a + b = 180^\circ \]
B.\[b + c = 180^\circ \]
C.\[c + d = 180^\circ \]
D.\[a + b + c = 180^\circ \]

Answer 1

Hint: Here, we have to find which of the given statements is true, knowing that AB is parallel to CD. We will use the property of parallel lines to find the supplementary angles and hence the required answer.

Complete step-by-step answer:
In the given figure, AB is parallel to CD.
But, if we see the arrows carefully then, the middle line which contains \[\angle b\] and \[\angle c\] , is parallel to both AB as well as CD.
Hence, these three lines are parallel to each other.
Now, as we know, when two parallel lines are intersected by another line (also known as transversal), then the angles present on one side of transversal and inside the two parallel lines are known as Consecutive interior angles.
Also, the consecutive interior angles are always supplementary angles, i.e. the measure of two consecutive interior angles always adds up to \[180^\circ \].
In this question, AB is parallel to the middle line as well as \[\angle a\] and \[\angle b\] are the angles present on one side of transversal and inside the two parallel lines, hence, \[\angle a\] and \[\angle b\] are consecutive interior angles.
So we can say that \[\angle a\] and \[\angle b\] are supplementary angles.
$\therefore \angle a+\angle b=180{}^\circ $
Hence, option A is true.

Note: In order to solve the question, we should know the properties of parallel lines. Some of the properties are listed below:
1.The corresponding angles of parallel lines are equal.
2.The Alternate interior angles, i.e. the angles inside the two parallel lines but on the opposite side of the transversal are also equal.
3.The Alternate exterior angles, i.e. the angles outside the two parallel lines but on the opposite side of the transversal are also equal.