Question

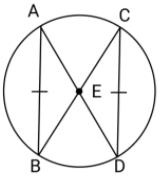
In the figure, $AB = CD$. Prove that $BE = DE$ and $AE = CE$ where $E$is the point of intersection of $AD$ and $BC$.

Answer 1

Hint:
For proving this question, we will use the criteria by comparing both the triangles. And here we will have the use of angles in the same segment and by seeing all the sides and angles ASA criteria of congruence will be held and in this way we can prove it.

Complete step by step solution:
 According to the question,
In $\vartriangle AEB$and $\vartriangle CED$, we have
Due to the angles in the same segment
$ \Rightarrow \angle BAE = \angle DCE$
And,
$ \Rightarrow \angle ABE = \angle CDE$, again due to the angles in the same segment.
And also $AB = CD$
After seeing all these three criteria, we can say that
$ASA$(Angle side angle), the criterion of congruence held here
Therefore, we can say that$\vartriangle AEB$ is congruent $\vartriangle CED$.
So because of the congruence
$ \Rightarrow AE = CE$, and also$BE = DE$.

Therefore, it is proved that$AE = CE$, and also$BE = DE$.

Additional information:
$ASA$ refers to a triangle where two angles and the length of the side between those two angles are given. $AAS$, refers to two angles, and the length of one of the sides not between the two angles is given.
The size of the third angle can be found by subtracting the sum of the other two angles ${180^ \circ }$ so the triangle is unique and solvable in either case. In fact, for this reason, we usually just say $AAS$ regardless of which side is given.

Note:
We see that this type of question gets solved by using congruence and here the diagram study plays an important role. We have to see the angle and the sides and then the congruence criterion held. And through this, we can prove it.