Question

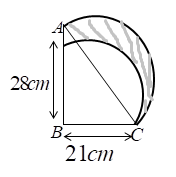
In the fig, ABC is a right-angled triangle, $\angle B = {90^0},$ AB = 28 cm and BC = 21cm. With AC as diameter, a semicircle is drawn and with BC as radius a quarter circle is drawn. Find the area of the shaded region.

Answer 1

Hint- From the figure, we can say that there are three visual shapes one is a triangle and other are two semi-circles. It is a simple mensuration problem in which we will use a formula of area right angled triangle and that of semicircle.

Complete step-by-step answer:
Formula used- Area of right angle triangle
$ = \dfrac{1}{2} \times base \times altitude$
Area of the semi-circle
$ = \dfrac{1}{2}\left( {\pi {r^2}} \right)$
Where r is the radius of the circle
Area of the semi-circle
In triangle ABC the hypotenuse is the diameter of the semicircle, there first we will calculate the diameter using the Pythagoras theorem
$
  A{C^2} = A{B^2} + B{C^2} \\
  A{C^2} = {28^2} + {21^2} \\
  AC = \sqrt {1225} \\
  AC = 35cm \\
$
Therefore the radius of the semi-circle is given by
$
  r = \dfrac{{AC}}{2} \\
  r = \dfrac{{35}}{2} = 17.5cm \\
$
Now, the area of the semi-circle is given by
$ = \dfrac{1}{2}\left( {\pi {r^2}} \right)$
Substituting the value of radius in the above equation, we get
$
   = \dfrac{1}{2}\left( {\pi {r^2}} \right) \\
   = \dfrac{1}{2} \times \pi \times {\left( {17.5} \right)^2} \\
   = 480.8c{m^2} \\
$
Now, the area of the quarter circle is given by
$ = \dfrac{1}{4}\left( {\pi {r^2}} \right)$
Substituting the value of the radius in the above equation, we get
$
   = \dfrac{1}{4}\left( {\pi {r^2}} \right) \\
   = \dfrac{1}{4} \times \pi \times {\left( {21} \right)^2} \\
   = 346.2c{m^2} \\
$
Area of the triangle is
$ = \dfrac{1}{2} \times base \times altitude$
Substituting the value of base and height from the figure, we get
$
   = \dfrac{1}{2} \times 21 \times 28 \\
   = 294c{m^2} \\
$
Now, we will calculate the area of the shaded region
The area of the shaded region is equal to sum of the area of the semi-circle and the area of the triangle – area of the quarter circle
= area of the semi-circle + area of the triangle – area of the quarter circle
Substituting the value of the areas calculated above in the equation, we get
$
   = 480.82 + 294 - 364.2 \\
   = 428.6c{m^2} \\
$
Hence, the area of the shaded region is $428.6c{m^2}$

Note- In order to solve these types of questions. Learn all the formulas related to the area of the triangle semi-circle. Since the semi- circle is the half of the circle and the quarter circle is the one fourth of the circle. So in order to find the area of the semi- circle and quarter circle, we will find the area of the circle then half it and one fourth it respectively. Draw the figure to get better visualization of the problem.