Question

In the diagram, the circle contains the vertices A, B, C of △ABC. Now \[\angle ABC=30{}^\circ \] and the length of AC is 5. The diameter of the circle is

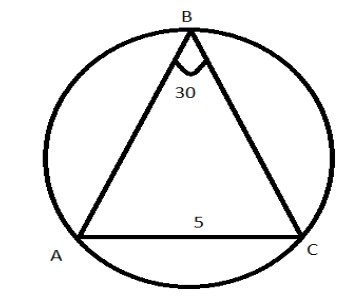
(a) $5\sqrt{3}$
(b) 8
(c) 10
(d) $5\sqrt{5}$

Answer 1

Hint: In this problem, we are given a triangle inscribed in a circle having one side length as 5 and one angle as 30°. To calculate the diameter of the circle, we must try to evaluate the radius of the circle by using some construction and geometrical properties.

Complete step-by-step answer:
Considering O as the center of the circle, join OA and OC.

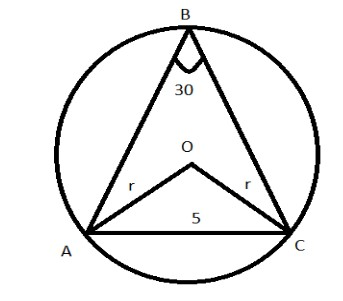
Using the theorem, “Angle subtended by the chord at the center is double the angle subtended at the circumference”. We can calculate the measurement of $\angle BAC$. Therefore, $\angle AOC= 2\angle BAC={{60}^{\circ }}$.
Now, we have to prove $\Delta AOC$ is an equilateral triangle. Length of $AC=5cm$ is given. Sides of the equilateral triangle are equal. The length of OA, OB and AC are equal.
The diameter of the circle is twice the radius.
In $\Delta ABC$, the angle ABC is 30 degrees.
Also, \[~\angle AOC=2\angle BAC={{60}^{\circ }}\].
In $\Delta OAC$,
OA = OC (radius of the circle). This implies that the respective angles must be equal.
$\therefore \angle OAC=\angle OCA$
Now, as we know that the sum total of all the angles of a triangle is 180 by angle sum property.
$\begin{align}
  & \angle OAC+\angle OCA+\angle AOC=180{}^\circ \\
 & \because \angle AOC=60{}^\circ ,\therefore \angle OAC=\angle OCA=60{}^\circ \\
\end{align}$
Hence, triangle OAC is equilateral.
Since, all the sides of an equilateral triangle are equal. Therefore, $OA=OC=AC=5$.
Thus, the diameter of the circle will be $2\times 5=10$.
Hence, option (c) is correct.

Note: The key concept for solving this problem is the knowledge of equilateral triangles and basic properties of angle subtended in a circle. Once the constructed triangle is proved equilateral, then by using the properties of the equilateral triangle we obtain our solution without any error.