Question

In the diagram, AB and AC are tangents to a circle, center O and radius 3.6cm. Calculate the area of the shaded region, given that $\left| \!{\underline {\,
  {BOC} \,}} \right. = \dfrac{{2\pi }}{3}radians$

Answer 1

Hint: The basic concepts involved in this question are:
Sector: A sector is a region enclosed between two radii and an arc in a circle. (In the above figure, OBC is a sector). The area of a sector can be found out by using the formula;
$\dfrac{\theta }{{360^\circ }} \times \pi {r^2}$= area where r= radius of the circle and $\theta $is the angle enclosed between the two radii.
Tangents: The tangents drawn to a circle from an exterior point are equal. (In the above figure, AB=AC)
The line drawn from center of the circle to the point of intersection of the tangent and the circle is normal to the tangent which means $\left| \!{\underline {\,
  {OBA} \,}} \right. = \dfrac{\pi }{2}$

Complete step-by-step answer:
To solve this question and to find the area of the shaded region, we will first find the area of the entire
quadrilateral OABC and then subtract the area of the sector.
Let’s draw the diagram and join vertices O and A.

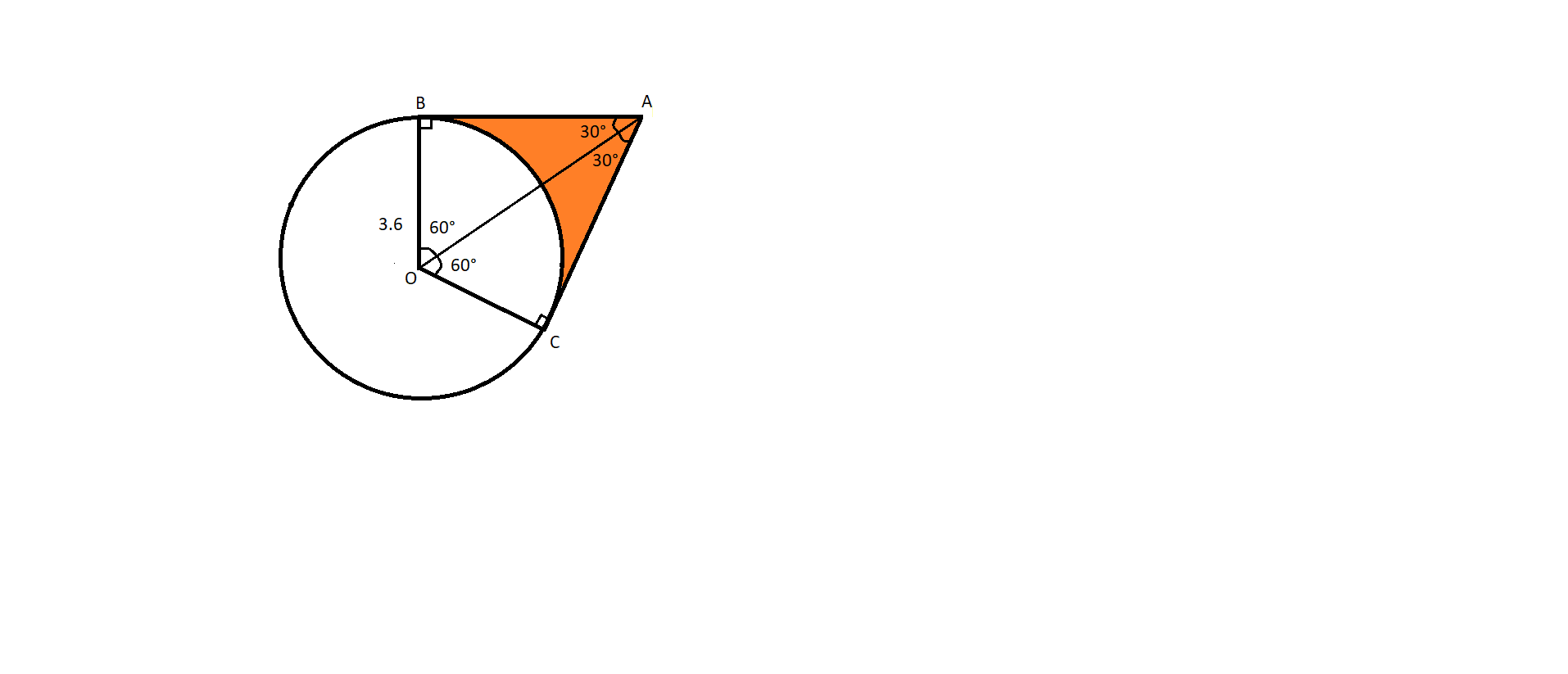
The triangles OBA and OCA are right-angled triangles with right angles at B and C.
We know that $\left| \!{\underline {\,
  {BOC} \,}} \right. = \dfrac{{2\pi }}{3}radians$
Because;
AB = AC (since tangents drawn from an external point to a circle are equal)
Therefore, angles opposite to the sides AB and AC are also equal, $\left| \!{\underline {\,
  {BOA} \,}} \right. = \left| \!{\underline {\,
  {COA} \,}} \right. $
Hence, $\left| \!{\underline {\,
  {BOA} \,}} \right. = \left| \!{\underline {\,
  {COA} \,}} \right. = 60^\circ $
In a triangle, the sum of the angles = 180°, $\left| \!{\underline {\,
  {OAB} \,}} \right. = 30^\circ $
Since the sides OB and OC are radii of a circle, they are equal hence the angles opposite to them are also
equal. So, $\left| \!{\underline {\,
  {OAB} \,}} \right. = \left| \!{\underline {\,
  {OAC} \,}} \right. = 30^\circ $
Now let’s find the length of AB.
We know that triangle OAB is a right-angled triangle with a right angle at B.
Using trigonometric ratios, we can find the length of AB.
$\tan 60^\circ = \dfrac{{AB}}{{OB}}$
$AB = OB \times \sqrt 3 = 3.6\sqrt 3 $
$AB = 6.235cm$
Now we have all the required lengths and angles:
$AB = 6.235cm$
$\left| \!{\underline {\,
  {BOA} \,}} \right. = \left| \!{\underline {\,
  {COA} \,}} \right. = 60^\circ $
$\left| \!{\underline {\,
  {OAB} \,}} \right. = \left| \!{\underline {\,
  {OAC} \,}} \right. = 30^\circ $
To find the area of the figure OABC, let’s divide it into two triangles OAB and OAC
The two triangles have equal areas since they have same height and base lengths.
The area of the triangle:
\[Base{\text{ }} = {\text{ }}OB{\text{ }} = {\text{ }}3.6cm\]
\[Height{\text{ }} = {\text{ }}AB{\text{ }} = {\text{ }}6.235cm\]
$area = \dfrac{1}{2}bh = 0.5 \times 3.6 \times 6.235 = 11.223c{m^2}$
Now the area of the entire quadrilateral OABC is equal to twice the area of the triangle;
$2 \times (11.223) = 22.446c{m^2}$= area of OABC
The area of the sector OBC = $\dfrac{\theta }{{360^\circ }} \times \pi {r^2}$
Here,$\theta = 120^\circ $
Therefore, area = $\dfrac{{120^\circ }}{{360^\circ }} \times \pi {(3.6)^2} = 13.557c{m^2}$
Since we have all the required areas;
Sector: 13.557
Quadrilateral: 22.446 (all the areas are in $c{m^2}$)
Area of the shaded region = $22.446 - 13.557 = 8.889c{m^2}$

Note: The above question involves testing all the fundamental concepts related to sectors, tangents and circles. It is better to remember the formula of area of sector and trigonometric ratios in a triangle which makes the calculation simple and small. The line passing through the center and is perpendicular to the tangent is called a normal to the tangent. We can also prove that $\left| \!{\underline {\,
  {BOA} \,}} \right. = \left| \!{\underline {\,
  {COA} \,}} \right. $ by using congruence of triangles OAB and OAC.