Question

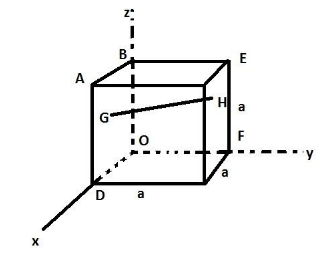
In the cube of side ' $ a $ ' shown in the figure, the vector from the central point of the face ABOD to the central point of the face BEFO will be:

(A) $ \dfrac{1}{2}a\left( {\hat i - \hat k} \right) $
(B) $ \dfrac{1}{2}a\left( {\hat j - \hat i} \right) $
(C) $ \dfrac{1}{2}a\left( {\hat k - \hat i} \right) $
(D) $ \dfrac{1}{2}a\left( {\hat j - \hat k} \right) $

Answer 1

Hint: In geometry, a position or position vector, also known as location vector or radius vector, is a Euclidean vector that represents the position of a point P in space in relation to an arbitrary reference origin O. Calculate the coordinates of the mid-points of the faces and compute them in the formula for position vector.

Formula Used: The formulae used in the solution are given here.
Position vector $ \vec r = x\hat i + y\hat j + z\hat k $
Where,
 $ \hat i $ = unit vector along x-direction,
 $ \hat j $ = unit vector along y-direction,
 $ \hat k $ = unit vector along z-direction.

Complete Answer:
It has been given that the length of the sides of the cube is $ a $ .
The centre of face ABOD is represented by point G as shown in the figure provided in the question. Similarly, the point H is the centre of the face BEFO of the cube. The line segment joining the two points on the opposite faces has been shown as the GH line.
The position vector is used to specify the position of a certain body. Knowing the position of a body is vital when it comes to describing the motion of that body. The position vector of an object is measured from the origin, in general.
Position vector $ \vec r = x\hat i + y\hat j + z\hat k $
Where,
 $ \hat i $ = unit vector along x-direction
 $ \hat j $ = unit vector along y-direction
 $ \hat k $ = unit vector along z-direction
In the given figure, the coordinate of point O is (0,0,0), point D is (a,0,0), and B is(0,0,a). The coordinates of point G is therefore, $ \left( {\dfrac{a}{2},0,\dfrac{a}{2}} \right) $ .
The coordinates of point F is (0,a,0) and thus, the coordinates of point H is $ \left( {0,\dfrac{a}{2},\dfrac{a}{2}} \right) $
The value of the required vector is given by, $ \mathop {GH}\limits^ \to = \vec H - \vec G $ .
The vector $ \vec H = 0\hat i + \dfrac{a}{2}\hat j + \dfrac{a}{2}\hat k $ and the vector $ \vec G = \dfrac{a}{2}\hat i + 0\hat j + \dfrac{a}{2}\hat k $ .
The vector $ \mathop {GH}\limits^ \to $ is given by,
 $ \mathop {GH}\limits^ \to = \left( {{x_2} - {x_1}} \right)\hat i + \left( {{y_2} - {y_1}} \right)\hat j + \left( {{z_2} - {z_1}} \right)\hat k $
Assigning the respective values in the equation, we get,
 $ \overrightarrow {GH} = \left( {0 - \dfrac{a}{2}} \right)\hat i + \left( {\dfrac{a}{2} - 0} \right)\hat j + \left( {\dfrac{a}{2} - \dfrac{a}{2}} \right)\hat k $
 $ \overrightarrow {GH} = \dfrac{a}{2}\hat i + \dfrac{a}{2}\hat j + 0\hat k $
Rearranging the values we get,
 $ \overrightarrow {GH} = \dfrac{1}{2}a\left( {\hat j - \hat i} \right) $ .
Hence the correct answer is Option B.

Note:
In three dimensions, any set of three-dimensional coordinates and their corresponding basis vectors can be used to define the location of a point in space—whichever is the simplest for the task at hand may be used. The position in a three-dimensional space is defined with respect to the coordinates of the points joining the two.