Question

In the circular table cover of 32cm, a design is formed, leaving an equilateral triangle ABC in the middle, as shown in the figure below. Find the area of the design (Shaded region).

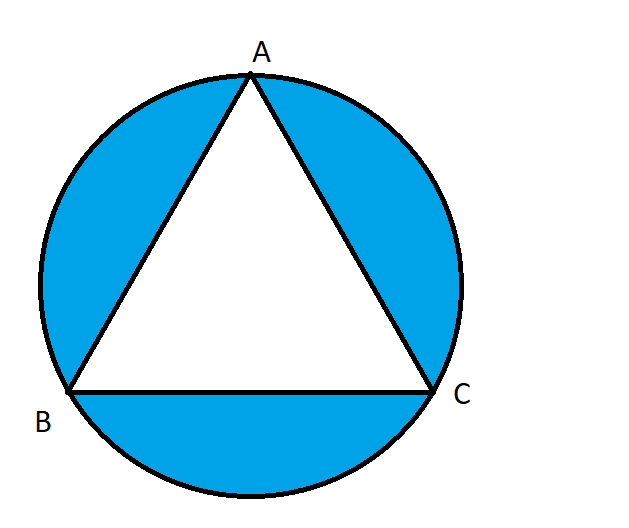
[a] $\left( \dfrac{16148}{7}-218\sqrt{3} \right)c{{m}^{2}}$
[b] $\left( \dfrac{19221}{7}-527\sqrt{3} \right)c{{m}^{2}}$
[c] $\left( \dfrac{6288}{7}-672\sqrt{3} \right)c{{m}^{2}}$
[d] None of these

Answer 1

Hint: Observe that the shaded region is the region of the circle excluding the triangular portion. Hence the area of the shaded region will be equal to the equilateral triangle subtracted from the area of the circle. From the centre of the circle (say O) draw a line (OD) perpendicular to BC and Join OB. Use the fact that the angle subtended by a chord at the centre is twice the angle subtended in the alternate segment to determine $\angle BOD$. In the triangle BOD, use trigonometry to determine BD and hence determine the length of the side BC. Use the fact that the area of an equilateral triangle of side length a is $\dfrac{\sqrt{3}}{4}{{a}^{2}}$. Hence determine the area of the equilateral triangle and hence the area of the shaded region.

Complete step-by-step answer:

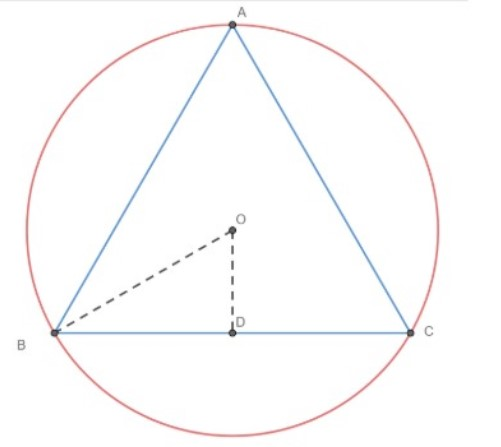
Construction: Draw OD perpendicular BC and join OB.
Now, since $\angle BAC$ is the angle in the alternate segment, we have $\angle BOC=2\angle BAC$
Since OD is the angle bisector of $\angle BOC$, we have $\angle BOD=\dfrac{1}{2}\angle BOC=\dfrac{1}{2}\left( 2\angle BAC \right)=\angle BAC$.
Since the measure of an angle of an equilateral triangle is $60{}^\circ $, we have
$\angle BOD=\angle BAC=60{}^\circ $
Now, we have in triangle OBD,
BD is the side opposite to O and OB is the hypotenuse
Hence, we have
$\sin \left( 60{}^\circ \right)=\dfrac{BD}{OB}$
Now, we have $\sin 60{}^\circ =\dfrac{\sqrt{3}}{2}$ and $OB=r=32$
Hence, we have
$\dfrac{BD}{32}=\dfrac{\sqrt{3}}{2}\Rightarrow BD=16\sqrt{3}$
Now, we have BC = 2BD $=32\sqrt{3}$
Now, we know that the area of an equilateral triangle of side a is given by $A=\dfrac{\sqrt{3}}{4}{{a}^{2}}$
Hence, we have
$ar\left( \Delta ABC \right)=\dfrac{\sqrt{3}}{4}{{\left( 32\sqrt{3} \right)}^{2}}=768\sqrt{3}$
Also the area of the circle $=\pi {{r}^{2}}=\dfrac{22}{7}\times {{32}^{2}}=\dfrac{22528}{7}$
Observe that the shaded region is the region of the circle excluding the triangular portion. Hence the area of the shaded region will be equal to the equilateral triangle subtracted from the area of the circle.

Hence the area of the shaded region $=\dfrac{22528}{7}-768\sqrt{3}$
Hence option [d] is correct.

Note: [1] In these types of questions, we need to identify which areas can be calculated from standard formulae. Then we need to think about how the required area can be found using the calculated areas. Like in the above case, the area of the shaded region cannot be calculated directly from standard formulae, but once we observe that this area is the difference of the area of the circle and the triangle, we easily calculate the area of the region.