Question

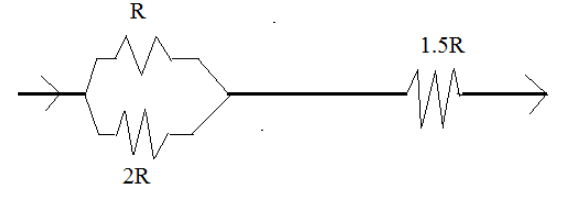
In the circuit diagram, heat produces in R, 2R and 1.5R are in the ratio of:

(A) 4:2:3
(B) 8:4:27
(C) 2:4:3
(D) 27:8:4

Answer 1

Hint: In this question, we need to determine the ratio of the heat produced in the resistances R, 2R and 1.5R such that it should satisfy all the conditions given in the figure. For this, we will use the relation between the heat, current and resistance. Moreover, the current division rule should be applied to determine the expression for the current in different resistances.

Complete step by step answer:
Let “I” be the total amount of current flowing through the circuit.
The starting and the endpoints of the resistances “R” and “2R” are the same, and so, we can say that the resistances “R” and “2R” are connected in parallel. As the resistances “R” and “2R” are connected in parallel, the voltage across them is the same, and the total current will be divided among them proportionally. Amount of current flowing through the resistance “R” is given as:
$
{I_R} = \left( {\dfrac{R}{{R + 2R}}} \right)I \\
\Rightarrow{I_R}= \dfrac{I}{3} - - - - (i) \\
 $
Similarly, the amount of current flowing the resistance “2R” is given as:
$
{I_{2R}} = \left( {\dfrac{{2R}}{{R + 2R}}} \right)I \\
\Rightarrow{I_{2R}}= \dfrac{{2I}}{3} - - - - (ii) \\
 $
Also, the current through the resistance “1.5R” is the total current, i.e., “I”.
Now, the product of the square of the current with the resistance and the time results in the heat developed by the resistance. Mathematically, $H = {I^2}Rt$.
So, now we will evaluate the heat developed in each resistance.
The heat produced in the resistance “R” is given as:
$
{H_1} = {I_R}^2Rt \\
\Rightarrow{H_1}= {\left( {\dfrac{I}{3}} \right)^2}Rt \\
\Rightarrow{H_1}= \dfrac{{{I^2}Rt}}{9} - - - - (iii) \\
$
Similarly, the heat produced in the resistance “2R” is given as:
$
{H_2} = {I_{2R}}^2Rt \\
\Rightarrow{H_2}= {\left( {\dfrac{{2I}}{3}} \right)^2}\left( {2R} \right)t \\
\Rightarrow{H_2}= \dfrac{{8{I^2}Rt}}{9} - - - - (iv) \\
 $
Again, the heat produced in the resistance “1.5R” is given as:
$
{H_3} = {I_{1.5R}}^2Rt \\
\Rightarrow{H_3} = {\left( I \right)^2}\left( {1.5R} \right)t \\
\Rightarrow{H_3}= \dfrac{{3{I^2}Rt}}{2} - - - - (v) \\
$
Now, taking the ratio of the heat produced by the resistance is given as:
$
{H_1}:{H_2}:{H_3} = \dfrac{{{I^2}Rt}}{9}:\dfrac{{8{I^2}Rt}}{9}:\dfrac{{3{I^2}Rt}}{2} \\
\Rightarrow{H_1}:{H_2}:{H_3} = \dfrac{1}{9}:\dfrac{8}{9}:\dfrac{3}{2} \\
\therefore{H_1}:{H_2}:{H_3}= 8:4:27 \\
$
Hence, the ratio of the heat produced in the resistances R, 2R and 1.5R are 8:4:27.Thus,
option B is correct.

Note:Students must be careful while applying the current division rule or the voltage division rule. The current division rule can only be applied to the resistances which have the same voltage across them while the voltage division rule can be applied to the resistances which have the same current through them.