Question

In the centre of a rectangular plot of land of dimensions \[120{\rm{m}} \times 100{\rm{m}}\], a rectangular portion is to be covered with trees so that the area of the remaining part of the plot is \[10500{{\rm{m}}^2}\]. Find the dimensions of the area to be planted. Which social act is being discussed here? Give its advantages.

Answer 1

Hint: Here, we need to find the dimensions of the area to be planted. We will assume the distance between the sides of the rectangular plot, and the sides of the rectangular portion to be covered by trees remains the same as \[x\] metres. Find the area to be planted both in metre squares and in terms of \[x\].

Complete step by step solution:
The trees are planted in the centre of the rectangular plot.
The distance between the sides of the rectangular plot, and the sides of the rectangular portion to be covered by trees remains the same.
Let the distance between the sides of the rectangular plot, and the sides of the rectangular portion to be covered by trees remains the same be \[x\] metres.
First, we will draw the diagram for this question.

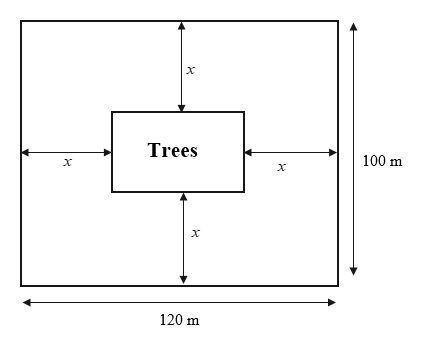
Here, we can observe that the rectangular portion to be covered by trees is equidistant from the sides of the rectangular plot. The distance is \[x\] metres.
Now, the area of a rectangle is the product of its length and breadth.
Therefore, we can find the area of the rectangular plot.
Substituting \[{\rm{length}} = 120{\rm{m}}\] and \[{\rm{breadth}} = 100{\rm{m}}\], we get
\[{\rm{Area \; of \; rectangular \; plot}} = 120{\rm{m}} \times 100{\rm{m}} = 12000{{\rm{m}}^2}\]
Next, we know that the area of the plot not covered by trees is \[10500{{\rm{m}}^2}\].
We can find the area to be planted by subtracting the area of the plot not covered from trees from the total area of the rectangular plot.
Therefore, we get the area to be planted as \[12000{{\rm{m}}^2} - 10500{{\rm{m}}^2} = 1500{{\rm{m}}^2}\]
Now, from the diagram, we can find the length and breadth of the area to be planted.
\[{\rm{Length}} = \left( {120 - x - x} \right){\rm{m}} = \left( {120 - 2x} \right){\rm{m}}\]
\[{\rm{Breadth}} = \left( {100 - x - x} \right){\rm{m}} = \left( {100 - 2x} \right){\rm{m}}\]
Therefore, we get the area to be planted as
\[{\rm{Area to be planted}} = \left( {120 - 2x} \right)\left( {100 - 2x} \right)\]
Substituting the area to be planted as \[1500{{\rm{m}}^2}\], we get
\[\left( {120 - 2x} \right)\left( {100 - 2x} \right) = 1500\]
Simplifying the equation, we get
\[\begin{array}{l} \Rightarrow 12000 + 4{x^2} - 200x - 240x = 1500\\ \Rightarrow 4{x^2} - 440x + 10500 = 0\\ \Rightarrow {x^2} - 110x + 2625 = 0\end{array}\]
This is a quadratic equation. We will factorise the equation to get the value of \[x\].
Factoring the quadratic equation, we get
\[\begin{array}{l} \Rightarrow {x^2} - 75x - 35x + 2625 = 0\\ \Rightarrow x\left( {x - 75} \right) - 35\left( {x - 75} \right) = 0\\ \Rightarrow \left( {x - 75} \right)\left( {x - 35} \right) = 0\end{array}\]
Therefore, either \[x - 75 = 0\] or \[x - 35 = 0\], that is either \[x = 35{\rm{ or }}75\].
However, if \[x = 75\], then length of the area to be planted will be
\[{\rm{Length}} = \left( {120 - 2 \times 75} \right){\rm{m}} = - 30{\rm{m}}\]
This is not possible as length cannot be negative.
Therefore, we get the value of \[x\] as 35 m.
Substituting 35 for \[x\] in the expressions for length and breadth of the area to be planted, we get
\[{\rm{Length}} = \left( {120 - 2 \times 35} \right){\rm{m}} = \left( {120 - 70} \right){\rm{m}} = 50{\rm{m}}\]
\[{\rm{Breadth}} = \left( {100 - 2 \times 35} \right){\rm{m}} = \left( {100 - 70} \right){\rm{m}} = 30{\rm{m}}\]

Therefore, the dimensions of the area to be planted are \[50{\rm{m}} \times 30{\rm{m}}\].

Additional Information
The social act of planting trees is being discussed here. This is also known as afforestation.
Planting trees is good for the environment.
Trees help in converting the carbon dioxide in the air to oxygen, and thus refreshing the air for us to breathe. This exchange of gases is important for us to survive.
Trees also give us various foods and products like resin.
Planting trees results in better quality of air, and prevents soil erosion.
Various wildlife animals also depend on trees for their survival.

Note:
We need to understand that we need to find the dimensions of the rectangular portion, not the area. We will make a mistake if we leave the answer at \[1500{{\rm{m}}^2}\]. Also, we should know how to properly factorise the obtained quadratic equation and when to apply zero product property for finding the value.