
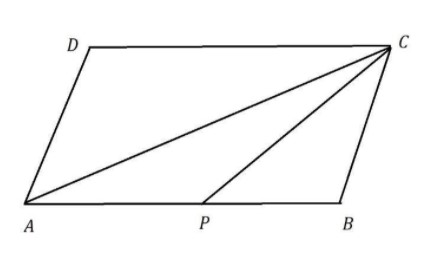
In the below figure, $ABCD$ is a parallelogram and $P$ is a mid-point of $AB$. If the area of a quadrilateral $APCD$ is $36c{m^2}$ , then what is the area of $\vartriangle ABC$?
A.$36c{m^2}$
B.$48c{m^2}$
C.$24c{m^2}$
D.None of these

Answer
574.2k+ views
Hint:Diagonal will bisect the area of the parallelogram and the line $PC$ will bisect the area of $\vartriangle ABC$.And in the quadrilateral $APCD$, area of $\vartriangle APC$ is one third of it. In this way you can find out the area of $\vartriangle ABC$.
Complete step-by-step answer:
Let us note down the given data initially,
$ABCD$ is a parallelogram and $P$ is a mid-point of $AB$.
area of quadrilateral $APCD$ is $36c{m^2}$.
We are asked to find out the area of $\vartriangle ABC$.
We know that in a parallelogram, Diagonal will bisect the area of the parallelogram.
So, area of $\vartriangle ADC$ $ = $ area of $\vartriangle ABC$.
In the $\vartriangle ABC$, the side $PC$ is the median.
We all know that median also bisects the area of a triangle.
Hence area of $\vartriangle APC$ $ = $ area of $\vartriangle PBC$.
From the above equations we can conclude that,
Area of quadrilateral $APCD$ $ = $ $3 \times $ Area pf $\vartriangle APC$.
Then, Area of $\vartriangle APC$ $ = \dfrac{1}{3} \times 36= 12c{m^2}$
Now,
Area of $\vartriangle ADC$ $ = $ Area of quadrilateral $APCD$ $ - $ Area of $\vartriangle APC$.
$
= 36 - 12 \\
= 24c{m^2} \\
$
But we already seen that the area of $\vartriangle ADC$ is equal to the area of $\vartriangle ABC$.
Hence, area of $\vartriangle ABC$ $ = $ area of $\vartriangle ADC = 24c{m^2}$
So, the correct answer is “Option C”.
Note:We can do this problem in a little bit different manner. In the above solution we found the area of $\vartriangle ADC$ by removing the area of $\vartriangle APC$ as it is one third of that. Then as we know that diagonal bisects the area of parallelogram, the area of $\vartriangle ADC$ is equal to the area of $\vartriangle ABC$. We can notice one thing that the area of quadrilateral $APCD$ is $\dfrac{2}{3}$ of the required area. By solving this proportionality also, we will get the same solution.
Complete step-by-step answer:
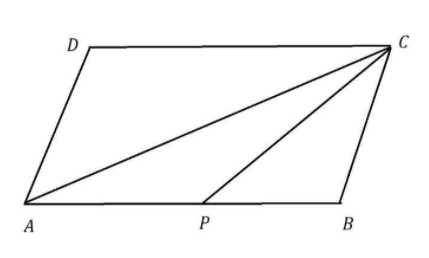
Let us note down the given data initially,

$ABCD$ is a parallelogram and $P$ is a mid-point of $AB$.
area of quadrilateral $APCD$ is $36c{m^2}$.
We are asked to find out the area of $\vartriangle ABC$.
We know that in a parallelogram, Diagonal will bisect the area of the parallelogram.
So, area of $\vartriangle ADC$ $ = $ area of $\vartriangle ABC$.
In the $\vartriangle ABC$, the side $PC$ is the median.
We all know that median also bisects the area of a triangle.
Hence area of $\vartriangle APC$ $ = $ area of $\vartriangle PBC$.
From the above equations we can conclude that,
Area of quadrilateral $APCD$ $ = $ $3 \times $ Area pf $\vartriangle APC$.
Then, Area of $\vartriangle APC$ $ = \dfrac{1}{3} \times 36= 12c{m^2}$
Now,
Area of $\vartriangle ADC$ $ = $ Area of quadrilateral $APCD$ $ - $ Area of $\vartriangle APC$.
$
= 36 - 12 \\
= 24c{m^2} \\
$
But we already seen that the area of $\vartriangle ADC$ is equal to the area of $\vartriangle ABC$.
Hence, area of $\vartriangle ABC$ $ = $ area of $\vartriangle ADC = 24c{m^2}$
So, the correct answer is “Option C”.
Note:We can do this problem in a little bit different manner. In the above solution we found the area of $\vartriangle ADC$ by removing the area of $\vartriangle APC$ as it is one third of that. Then as we know that diagonal bisects the area of parallelogram, the area of $\vartriangle ADC$ is equal to the area of $\vartriangle ABC$. We can notice one thing that the area of quadrilateral $APCD$ is $\dfrac{2}{3}$ of the required area. By solving this proportionality also, we will get the same solution.
Recently Updated Pages
In cricket, what is a "pink ball" primarily used for?

In cricket, what is the "new ball" phase?

In cricket, what is a "death over"?

What is the "Powerplay" in T20 cricket?

In cricket, what is a "super over"?

In cricket, what is a "tail-ender"?

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

Write an application to the principal requesting five class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Who Won 36 Oscar Awards? Record Holder Revealed




