Question

In the below diagram, find $\angle QRS$, where PQRS is a cyclic quadrilateral whose diagonals intersect at O and $\angle SQR={{60}^{\circ }}$ and $\angle RPQ={{40}^{\circ }}$.

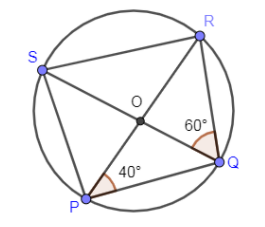
Answer 1

Hint: In the above problem, we have given $\angle SQR={{60}^{\circ }}$ so $\angle SPR$ is also ${{60}^{\circ }}$ because angles subtended in the same segment are equal and here the same segment is SR. Now, we got the angle $\angle SPR$ then we will find $\angle SPQ$ which is equal to the sum of the angles $\angle SPR\And \angle RPQ$. After that we are going to use the property of cyclic quadrilateral which says that opposite angles of the quadrilateral are ${{180}^{\circ }}$. Then the sum of the opposite angles $\angle SPQ\And \angle QRS$ is equal to ${{180}^{\circ }}$ and we know the value of angle SPQ and from this equation, we will find the angle QRS.

Complete step-by-step solution:
The figure which is given in the above problem is as follows:

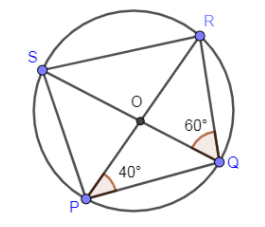
Now, if you look at the above figure, you will find that on the same segment SR, the two angles $\angle SPR\And \angle SQR$ are lying and these two angles are equal due to the property that angles on the same segment are equal.
$\angle SPR=\angle SQR={{60}^{\circ }}$
Now, we are going to mark the angle $\angle SPR={{60}^{\circ }}$ in the above figure, and then the figure will look as follows:

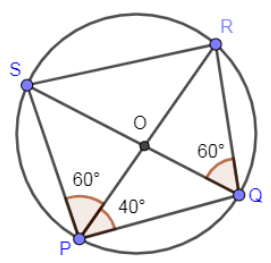
As you can see from the above figure that measurement of $\angle SPQ$ is equal to sum of angles SPR and angle RPQ.
$\begin{align}
  & \angle SPQ=\angle SPR+\angle RPQ \\
 & \Rightarrow \angle SPQ={{60}^{\circ }}+{{40}^{\circ }} \\
 & \Rightarrow \angle SPQ={{100}^{\circ }} \\
\end{align}$
It is given that PQRS is a cyclic quadrilateral and we know that sum of opposite angles of quadrilateral is ${{180}^{\circ }}$ so sum of angles SPQ and angle QRS is equal to ${{180}^{\circ }}$.
$\begin{align}
  & \angle SPQ+\angle QRS={{180}^{\circ }} \\
 & \Rightarrow {{100}^{\circ }}+\angle QRS={{180}^{\circ }} \\
 & \Rightarrow \angle QRS={{180}^{\circ }}-{{100}^{\circ }} \\
 & \Rightarrow \angle QRS={{80}^{\circ }} \\
\end{align}$
From the above solution, we got the value of $\angle QRS={{80}^{\circ }}$.

Note: This question demands the knowledge of the property that angles on the same segment are equal and also in a cyclic quadrilateral, the sum of the opposite angles of a quadrilateral is ${{180}^{\circ }}$, failure of any of the concepts will paralyze you to solve this problem. One more thing, don’t assume what is given in the figure for e.g. if you see the figure given in the above problem, you might assume O where diagonals intersect each other is the center of the circle but it does not so refrain yourself from making such mistakes.