Question

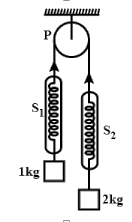
In the Atwood machine (data as in figure), P is a massless pulley, and springs \[{{S}_{1\text{ }}}\text{and }{{S}_{2}}\] are also massless. If the blocks are let go, the readings in \[{{S}_{1\text{ }}}\text{and }{{S}_{2}}\] will respectively be:

\[\begin{align}
  & \text{A}\text{. }\dfrac{1}{3}kg,\dfrac{2g}{3}kg \\
 & \text{B}\text{. }\dfrac{4g}{3}kg,\dfrac{4g}{3}kg \\
 & \text{C}\text{. }\dfrac{2g}{3}kg,\dfrac{4}{3}kg \\
 & \text{D}\text{. }\dfrac{2}{3}kg,\dfrac{2}{3}kg \\
\end{align}\]

Answer 1

Hint: Here we have to find reading for \[{{S}_{1\text{ }}}\text{and }{{S}_{2}}\] where both are the massless spring, when we let go the blocks, it will created a tension in the spring and the rope or the string. As the springs are massless it will only have tension. Therefore we have to find the tension in the spring. We can draw a simple diagram to find the force on the blocks and find the tension.

Complete answer:
We can replace the springs with the rope, as the springs are massless and it is attached between the rope and the block. The tension experienced by the spring will be the same as the tension created in the rope. As there is a single rope therefore the tension will be the same in both the springs. Hence the given diagram can be drawn as

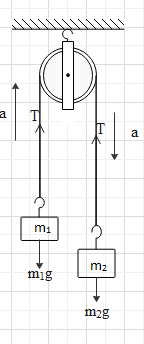
The forces experienced by the block of mass \[{{m}_{1}}\] are the upward tension, the downward gravitational pull and the upward force, then the equation for the block \[{{m}_{1}}\] is given as

\[{{m}_{1}}g-T={{m}_{1}}a\] ………….. (i)

Where g is acceleration due to gravity.
The forces experienced by the block \[{{m}_{2}}\]
are the upward tension, the downward gravitational pull and the downward force, then the equation for the block \[{{m}_{2}}\] is given as

\[T-{{m}_{2}}g={{m}_{2}}a\]………….. (ii)
Adding the both equations we get

\[\begin{align}
  & {{m}_{1}}g-{{m}_{2}}g={{m}_{1}}a+{{m}_{2}}a \\
 & \implies g({{m}_{1}}-{{m}_{2}})=a({{m}_{1}}+{{m}_{2}}) \\
 & \implies a=\dfrac{g({{m}_{1}}-{{m}_{2}})}{({{m}_{1}}+{{m}_{2}})} \\
\end{align}\]

We now get the value of acceleration with which system will move.
Substituting value of \[{{m}_{1}}\text{ and }{{m}_{2}}\]in the above equation, (\[{{m}_{1}}\text{=1}kg\text{ and }{{m}_{2}}=2kg\]) we get
\[\begin{align}
  & a=\dfrac{g(1-2)}{(1+2)} \\
 & \implies a=-\dfrac{g}{3} \\
\end{align}\]
Negative sign shows the downward direction of the acceleration.
Substituting value of a and \[{{m}_{1}}\text{=1}kg\] in equation (i) we will get the tension T
\[\begin{align}
  & g-T=a \\
 & \implies T=g-a \\
 & \implies T=g-\left( \dfrac{-g}{3} \right) \\
 & \implies T=g+\dfrac{g}{3} \\
 & \implies T=\dfrac{4g}{3}kg \\
\end{align}\]
Hence the reading for \[{{S}_{1}}\text{ and }{{S}_{2}}\]are \[\dfrac{4g}{3}kg\text{ and }\dfrac{4g}{3}kg\]respectively.

So, the correct answer is “Option B”.

Note:
Tension has a unit of force that is Newton. Here it is in kg because we have not substituted the value of g, therefore it is expressed in kilograms. Also acceleration will have the same unit as of acceleration due to gravity. The value of a is the net acceleration experienced by the string due to the movement of blocks.