Question

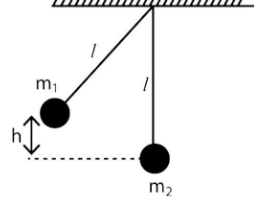
In the arrangement shown, the pendulum on the left is pulled aside. It is then released and allowed to collide with another pendulum which is at rest. A perfectly inelastic collision occurs and the system rises to a height $\dfrac{h}{4}$. The ratio of the masses $\dfrac{{{m_1}}}{{{m_2}}}$ of the pendulum is:

A. $1$
B. $2$
C. $3$
D. $4$

Answer 1

Hint: To solve this problem first of all we will find the initial velocity of the first mass which is present at height h then we will apply the moment conservation in order to get the final velocity of the combined system. At last we will substitute the value in order to get the ratio of their masses.

Complete step by step answer:
Let's have a quick overview of the pendulum before moving on to the question. A pendulum is a weight that may freely swing and is suspended from a pivot. Gravity operates as a restorative force when a pendulum is shifted sideways from its resting, equilibrium position, propelling the pendulum back to its equilibrium position.

Let us now attempt to answer the question;
So, for mass ${m_1}$ :
Velocity of mass \[{m_1}\] just before collision \[v = \sqrt {2gh} \]
After collision, the combined mass \[\left( {{m_1} + {m_2}} \right)\] moves with a common velocity \[V\] and reaches a height $\dfrac{h}{4}$ .
Using momentum conservation just before and after a collision: ${P_i} + {P_f}$
${m_1}v + 0 = \left( {{m_1} + {m_2}} \right)V \\
\Rightarrow {m_1}\sqrt {2gh} = \left( {{m_1} + {m_2}} \right)V \\
\Rightarrow V = \dfrac{{{m_1}\sqrt {2gh} }}{{{m_1} + {m_2}}}\,\,\,\,\,..........\left( 1 \right) \\ $
$\dfrac{{{m_1}\sqrt {2gh} }}{{{m_1} + {m_2}}} = \dfrac{{\sqrt {2gh} }}{2} \\
\Rightarrow {m_1} = {m_2} \\ $
Using the relation
$V = \sqrt {2g \times \dfrac{h}{4}} = \dfrac{{\sqrt {2gh} }}{2}\,\,in\left( 1 \right) \\
\Rightarrow \dfrac{{{m_1}\sqrt {2gh} }}{{{m_1} + {m_2}}} = \dfrac{{\sqrt {2gh} }}{2} \\
\therefore {m_1} = {m_2} \\ $
So, the correct option is A.

Note:Students should be very careful while solving these types of problems related to momentum conservation because momentum is conserved only when there is no external force acting on the system. If there was external force then we would have applied the other method.