Question

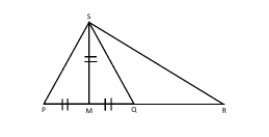
In the adjoining figure P, M, Q, R are collinear and PM = MQ = MS. $S{R^2} = PR .QR$. Then

A) $\angle SQR = \angle SMP$
B) $\angle QSR = \angle MSP$
C) $\angle QSR = \angle MSQ$
D) $\angle QSM = \angle PSM$

Answer 1

Hint:
It is given in the question that in the adjoining figure P, M, Q, R are collinear and PM = MQ = MS. $S{R^2} = PR.PQ$
Firstly, by the equation $S{R^2} = PR.PQ$ , we will proportionate the equation and note that as (I)
Then after, from the $\Delta SPR$ and $\Delta SQR$ we will get the answer as proportion and note that as (II)
Finally, we will compare equation (I) and equation (II) and we will get an answer.

Complete step by step solution:
It is given in the question that in the adjoining figure P, M, Q, R are collinear and PM = MQ = MS. $S{R^2} = PR.PQ$
 $\because PM = QM$
 $\therefore \angle PSM = \angle QSM$
$\because $ $S{R^2} = PR.PQ$
 $\therefore SR.SR = PR.PQ$
Now,
 $\therefore \dfrac{{SR}}{{PR}} = \dfrac{{QR}}{{SR}}$ (given) (I)
Now, In $\Delta SPR$ and $\Delta SQR$
$\therefore $$\dfrac{{SR}}{{PR}} = \dfrac{{QR}}{{SR}}$ (II)
Hence, from equation (I) and (II), we get,
 $\angle SQR = \angle SMP$
Hence, Proved.

Note:
Collinear Points: Three or more points are said to be collinear if they lie on a single straight line. A line on which points lie, especially if it is related to a geometric figure such as a triangle, is sometimes called an axis. Two points are trivially collinear since two points determine a line.