Question

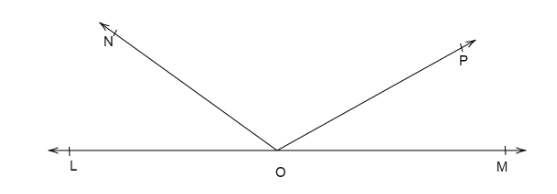
In the adjoining figure OL and OM are opposite rays. \[\angle LON + \angle MOP = {80^ \circ }\]. Find \[\angle NOP\].

Answer 1

Hint: Here we use the concept that opposite rays form a straight line and then we write the angles on that straight line. We use the concept of supplementary angles on a straight line. Using the given sum of two angles lying on the straight line we find the third angle lying on the straight line by writing the sum of all three angles equal to \[{180^ \circ }\].
* Opposite rays are the rays that are emerging from the same point but are in the exact opposite direction to each other.
* The sum of all angles lying on a straight line is \[{180^ \circ }\].

Complete step-by-step answer:
We know OL and OM are opposite rays which emerge from the point O and proceed in exact opposite direction to each other. We can say rays OL and OM form a straight line LM.
We know the angles on the straight line LM are \[\angle LON,\angle NOP,\angle MOP\]
Since, we know the sum of all angles lying on a straight line is equal to \[{180^ \circ }\]
We can write \[\angle LON + \angle NOP + \angle MOP = {180^ \circ }\] … (1)
We are given that \[\angle LON + \angle MOP = {80^ \circ }\]
Substitute the value of \[\angle LON + \angle MOP = {80^ \circ }\]in equation (1)
\[ \Rightarrow \angle NOP + {80^ \circ } = {180^ \circ }\]
Shift all constant values in degrees to RHS of the equation
\[ \Rightarrow \angle NOP = {180^ \circ } - {80^ \circ }\]
Calculate the value on RHS in degrees
\[ \Rightarrow \angle NOP = {100^ \circ }\]

Therefore,\[\angle NOP = {100^ \circ }\]

Note: Students many times make mistakes while shifting the values from one side of the equation to another side of the equation. Keep in mind signs of a value changes from negative to positive and vice-versa when shifting the value from one side of the equation to another side of the equation.