Question

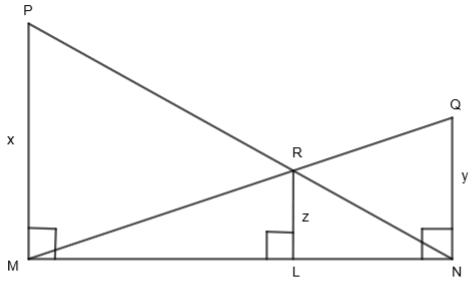
In the adjoining figure, MP, LR and NQ are the perpendiculars to the straight line MLN. If MP = x, LR = z and NQ = y, prove that \[\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{z}.\]
 

Answer 1

- Hint: First of all, prove \[\Delta NMP\text{ and }\Delta NLR\] similar and by equating the ratio of the corresponding sides, get, \[\dfrac{z}{x}=\dfrac{LN}{MN}\]. Similarly, prove \[\Delta MNQ\text{ and }\Delta MLR\] and get a relation between z and y. Now, add these two equations to get the required result.



Complete step-by-step solution -

In the given figure, MP, LR, and NQ are the perpendiculars to the straight line MLN. If MP = x, LR = z and NQ = y, we have to prove that \[\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{z}.\]

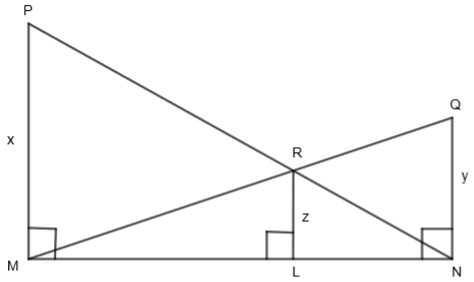
Let us consider \[\Delta NMP\text{ and }\Delta NLR\] from the given figure. We are given that MP and LR are perpendicular on line MLN. So, we get,
\[\angle PML=\angle RLN={{90}^{o}}\]
Also, \[\angle RNL\] is common to both the triangles, so we get,
\[\angle RNL=\angle RNL=\text{ Common Angles}\]
Hence, by AA or angle-angle property, \[\Delta NMP\] is similar to \[\Delta NLR\text{ or }\Delta NMP\sim \Delta NLR.\]
We know that the ratio of the corresponding sides of the similar triangles is equal. So, we get,
\[\dfrac{LR}{MP}=\dfrac{LN}{MN}\]
By substituting LR = x and MP = x, we get,
\[\dfrac{z}{x}=\dfrac{LN}{MN}....\left( i \right)\]
Let us consider \[\Delta MNQ\text{ and }\Delta MLR\]. We are given that LR and NQ are perpendicular on the line MLN. So, we get,
\[\angle MNQ=\angle MLR={{90}^{o}}\]
Also, \[\angle RML\] is common to both the triangles, so we get,
\[\angle RML=\angle RML=\text{ Common Angles}\]
Hence, by AA or angle-angle property, \[\Delta MNQ\] is similar to \[\Delta MLR\text{ or }\Delta MNQ\sim \Delta MLR.\]
We know that the ratio of the corresponding sides of similar triangles is equal. So, we get,
\[\dfrac{LR}{QN}=\dfrac{ML}{MN}\]
By substituting LR = z and QN = y, we get,
\[\dfrac{z}{y}=\dfrac{ML}{MN}....\left( ii \right)\]
By adding equation (i) and (ii), we get,
\[\dfrac{z}{x}+\dfrac{z}{y}=\dfrac{LN}{MN}+\dfrac{ML}{MN}\]
\[\dfrac{z}{x}+\dfrac{z}{y}=\dfrac{LN+ML}{MN}\]
By figure, we get LN + ML = MN. So, we get,
\[\dfrac{z}{x}+\dfrac{z}{y}=\dfrac{MN}{MN}\]
\[\Rightarrow z\left( \dfrac{1}{x}+\dfrac{1}{y} \right)=1\]
By dividing both the sides with z, we get,
\[\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{z}\]
Hence proved.
So, we have proved the required result.

Note: In this question, many students make mistakes while writing the corresponding sides of the similar triangles, so this must be taken care of. Also, remember that in case of similar triangles, we have to equate the ratio of the corresponding sides, while in case of the congruent triangle, we have to equate the value of the corresponding sides, so, we don’t get confused between the similarity and congruence of two triangles.