Question

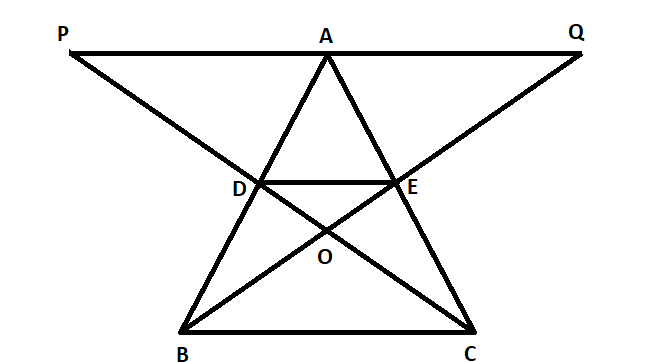
In the adjoining figure, D and E are respectively the mid points of sides AB and AC of $\vartriangle ABC$. If $PQ\parallel BC$ and CDP and BEQ are straight lines then prove that $ar(\vartriangle ABQ) = ar(\vartriangle ACP)$.

Answer 1

Hint: We will use the principle of midpoint theorem in this problem. The line segment joining the midpoints of two sides of a triangle is parallel to the third side and the line drawn through the midpoint of one side of a triangle, parallel to another side bisects the third side.

Complete step by step solution:
According to the question, we know that the D and E are mid points of AB and AC.
So we get, $DE\parallel BC\parallel PQ$.
Now we will consider $\vartriangle ACP$, we have $AP\parallel DE$ and E is the midpoint of AC.
Using the mid-point theorem we know that D is the midpoint PC.
Thus,
$DE = \dfrac{1}{2}AP$.
It can also be written as,
$AP = 2DE$. ………(i)
Let us consider $\vartriangle ABQ$, we have $AQ\parallel DE$ and D is the midpoint of AB.
Now, using the mid-point theorem we know that E is the mid-point of BQ.
So we get
$DE = \dfrac{1}{2}AQ$.
We can also write this as,
AQ=2DE. ………..(ii)
Using equations (i) and (ii), we get
AP = AQ.
Now, we know that $\vartriangle ACP$and $\vartriangle ABQ$ lie on the bases AP and AQ between the same parallels BC and PQ.
So we get,
Area of $\vartriangle ACP$= Area of $\vartriangle ABQ$.
Therefore, it is proved that $ar(\vartriangle ABQ) = ar(\vartriangle ACP)$.

Note: whenever we ask such questions, we first have to remember the concept of mid-point theorem. we will consider the triangles from the figure and then by using the theorem we will make some equations and then from those equations, we will prove the statements that are asked in the question.