Question

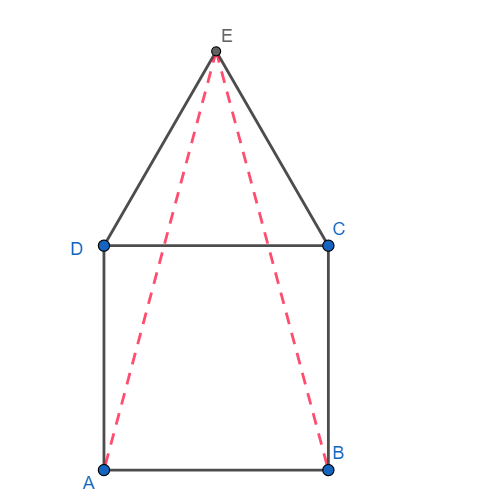
In the adjoining figure ABCD is a square and ECD is an equilateral triangle described on side DC. If $\angle DAE=\theta $ and AE = kBE, then

[a] $\theta =30{}^\circ ,k=1$
[b] $\theta =15{}^\circ ,k=2$
[c] $\theta =15{}^\circ ,k=1$
[d] $\theta =30{}^\circ ,k=2$

Answer 1

Hint: Use the fact that the angles of a square are $90{}^\circ $ each and the angles of an equilateral triangle are $60{}^\circ $ each. Hence find the measures of $\angle ADC$ and $\angle CDE$. Use the fact that $\angle ADC+\angle CDE=\angle ADE$ and hence find the measure of $\angle ADE$. Use the fact the angles opposite to equal sides of an isosceles triangle are equal and hence prove that $\angle DAE=\angle DEA$. Use the angle sum property of a triangle in the triangle ADE and hence find the measure of $\angle DAE$. Hence determine which of the option is correct.

Complete step by step answer:
Before solving the question, we need to understand the properties of a square and an equilateral triangle.
Equilateral triangle: A triangle is said to be an equilateral triangle if all its sides and angles are equal. The angles of an equilateral triangle are $60{}^\circ $ each.
Square: A quadrilateral is said to be a square if all its sides and angles are equal. Each angle of a square is $90{}^\circ $.
Given: ABCD is a square and EDC is an equilateral triangle on side DC of the square and $AE=kBE$
To determine: $\angle DAE$ and the value of k.
Since ABCD is a square, we have AD = DC.
Since $\Delta DCE$ is an equilateral triangle, we have $DC=DE$
Hence, we have AD = DE.
Now, in triangle DAE, we have DA = DE.
Hence, we have
$\angle DAE=\angle DEA$(The angles opposite to equal sides of a triangle are equal).
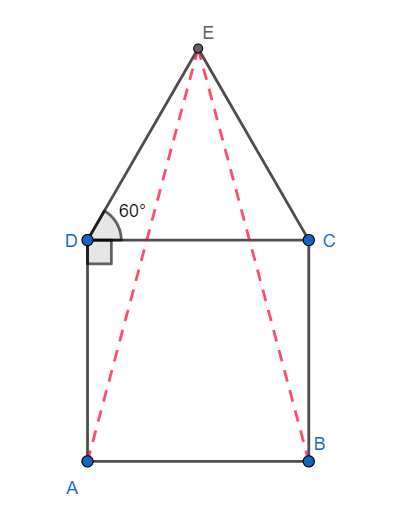
Since ABCD is a square, we have $\angle ADC=90{}^\circ $
Since $\Delta DCE$ is an equilateral triangle, we have $\angle CDE=60{}^\circ $
From the above diagram, we have $\angle ADC+\angle CDE=\angle ADE$
Hence, we have
$\angle ADE=90{}^\circ +60{}^\circ =150{}^\circ $
We know that the sum of angles of a triangle is equal to $180{}^\circ $
Applying angle sum property of a triangle in triangle ADE, we get
$\begin{align}
  & \angle DAE+\angle DEA+\angle ADE=180{}^\circ \\
 & \Rightarrow 2\angle DAE+150{}^\circ =180{}^\circ \\
 & \Rightarrow 2\angle DAE=30{}^\circ \\
 & \Rightarrow \angle DAE=15{}^\circ \\
\end{align}$
Hence, we have $\angle DEA=15{}^\circ $
Now, in triangles ADE and BCE, we have
AD = BC (Sides of the square)
$\angle ADE=\angle BCE\left( each\ 150{}^\circ \right)$
DE = CE (Sides of the equilateral triangle)
Hence, we have
$\Delta ADE\cong \Delta BCE$(By SAS congruence condition)
Hence, we have AE = BE (Corresponding parts of congruent triangles)
Hence, we have k = 1.
Hence option [c] is correct.

Note:
[1] The use of the congruences correctly is very important for the questions of this type. It must be noted that the angles of two triangles which are equal when applying SAS rule should be the angle included between the two sides which are shown equally as is done above. Many students do not take that into consideration and arrive at incorrect results.