
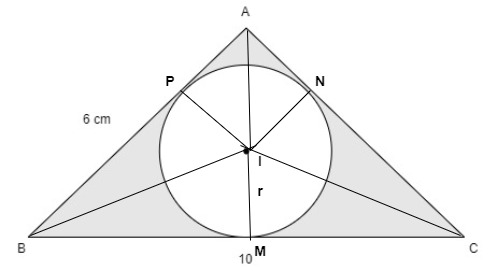
In the adjoining figure $ABC$ is a right angled at $A$. Find the area of the shaded region if $AB = 6{\text{ cm and }}BC = 10{\text{ cm}}$ and $I$ is the center of an incircle of $\vartriangle ABC$.

Answer
597.6k+ views
Hint – In order to find the area of the shaded region, we first have to find the perpendicular of the $\vartriangle ABC$ by using the Pythagoras theorem, then we will find its area and compare it to the three other triangles which are formed by joining the center of circle$\left( I \right)$ with every corner$\left( {A,B,C} \right)$ of the $\vartriangle ABC$. So, we will get the value of $r$(radius of circle) as it is the height of those three triangles. Then, we will find the area of the circle and subtract it from the area of $\vartriangle ABC$ to get the area of the shaded region.
Complete step-by-step answer:
$ABC$ is a right angled triangle at right angle at $A$. $AB = 6{\text{ cm and }}BC = 10{\text{ cm}}$.
Let $I$ be the center and $r$ be the radius of the incircle. $AB,{\text{ }}BC{\text{ and }}CA$ are tangents to the circle at $P,{\text{ }}M{\text{ and }}N$.
$\therefore IP = IM = IN = r$ (radius of the circle)
In right $\vartriangle ABC$,
By using the Pythagoras theorem, we get
$B{C^2} = A{B^2} + A{C^2}$ where, $BC$ is the hypotenuse, $AB$ is the base, $AC$ is the perpendicular.
$
\Rightarrow {10^2} = {6^2} + A{C^2} \\
\Rightarrow A{C^2} = 100 - 36 \\
\Rightarrow A{C^2} = 64 \\
$
By taking square root both sides,
$AC = \sqrt {64} = 8{\text{ cm}}$
Since, area of $\vartriangle ABC = \dfrac{1}{2} \times base \times height$ where, $base = AB = 6{\text{ cm and }}height = AC = 8{\text{ cm}}$
$ = \dfrac{1}{2} \times 8 \times 6 = 24{\text{ c}}{{\text{m}}^2}$
So, area of $\vartriangle ABC$= area of$\vartriangle IAB + $area of$\vartriangle IBC + $area of$\vartriangle ICA$
$ \Rightarrow 24 = \dfrac{1}{2} \times r \times AB + \dfrac{1}{2} \times r \times BC + \dfrac{1}{2} \times r \times CA$ where, $r$(radius of circle) is height and $AB,{\text{ }}BC{\text{ and }}CA$ are the base of the triangle accordingly.
Take $\dfrac{1}{2}r$ common from R.H.S
$
\Rightarrow 24 = \dfrac{1}{2}r\left( {AB + BC + CA} \right) \\
\Rightarrow 24 = \dfrac{1}{2}r\left( {6 + 10 + 8} \right) \\
\Rightarrow 24 = \dfrac{1}{2}{\text{r}} \times {\text{24 }} \\
$
By cross multiplying and simplifying, we get
$r = 2$
Since, area of the circle
$
= \pi {r^2} \\
= 3.14 \times 2 \times 2 = 12.56{\text{ c}}{{\text{m}}^2} \\
$ where, $\pi = \dfrac{{22}}{7} \simeq 3.14$
Now, area of the shaded region$ = $area of $\vartriangle ABC$$ - $area of circle
$
= 24 - 12.56 \\
= 11.44{\text{ c}}{{\text{m}}^2} \\
$
Hence, the area of the shaded region is $11.44{\text{ c}}{{\text{m}}^2}$.
Note – In these kind of questions, we should know what Pythagoras theorem i.e. ${h^2} = {b^2} + {p^2}$ .Also, we should know what are the formulas for circle and triangle i.e. area of circle$ = \pi {r^2}$ and area of triangle$ = \dfrac{1}{2} \times base \times height$ and their properties i.e. the line from the center of the circle to the point on the tangent of the circle where it touches the circle is always perpendicular to each other.
One must remember all these concepts and formulas to avoid the common mistakes like which is to be taken hypotenuse, base and perpendicular and the sides of the triangle are assumed as tangents to incircle. Also, one must do remember this method as it is the only approach to find the area of the shaded region.
Complete step-by-step answer:
$ABC$ is a right angled triangle at right angle at $A$. $AB = 6{\text{ cm and }}BC = 10{\text{ cm}}$.
Let $I$ be the center and $r$ be the radius of the incircle. $AB,{\text{ }}BC{\text{ and }}CA$ are tangents to the circle at $P,{\text{ }}M{\text{ and }}N$.
$\therefore IP = IM = IN = r$ (radius of the circle)
In right $\vartriangle ABC$,
By using the Pythagoras theorem, we get
$B{C^2} = A{B^2} + A{C^2}$ where, $BC$ is the hypotenuse, $AB$ is the base, $AC$ is the perpendicular.
$
\Rightarrow {10^2} = {6^2} + A{C^2} \\
\Rightarrow A{C^2} = 100 - 36 \\
\Rightarrow A{C^2} = 64 \\
$
By taking square root both sides,
$AC = \sqrt {64} = 8{\text{ cm}}$
Since, area of $\vartriangle ABC = \dfrac{1}{2} \times base \times height$ where, $base = AB = 6{\text{ cm and }}height = AC = 8{\text{ cm}}$
$ = \dfrac{1}{2} \times 8 \times 6 = 24{\text{ c}}{{\text{m}}^2}$
So, area of $\vartriangle ABC$= area of$\vartriangle IAB + $area of$\vartriangle IBC + $area of$\vartriangle ICA$
$ \Rightarrow 24 = \dfrac{1}{2} \times r \times AB + \dfrac{1}{2} \times r \times BC + \dfrac{1}{2} \times r \times CA$ where, $r$(radius of circle) is height and $AB,{\text{ }}BC{\text{ and }}CA$ are the base of the triangle accordingly.
Take $\dfrac{1}{2}r$ common from R.H.S
$
\Rightarrow 24 = \dfrac{1}{2}r\left( {AB + BC + CA} \right) \\
\Rightarrow 24 = \dfrac{1}{2}r\left( {6 + 10 + 8} \right) \\
\Rightarrow 24 = \dfrac{1}{2}{\text{r}} \times {\text{24 }} \\
$
By cross multiplying and simplifying, we get
$r = 2$
Since, area of the circle
$
= \pi {r^2} \\
= 3.14 \times 2 \times 2 = 12.56{\text{ c}}{{\text{m}}^2} \\
$ where, $\pi = \dfrac{{22}}{7} \simeq 3.14$
Now, area of the shaded region$ = $area of $\vartriangle ABC$$ - $area of circle
$
= 24 - 12.56 \\
= 11.44{\text{ c}}{{\text{m}}^2} \\
$
Hence, the area of the shaded region is $11.44{\text{ c}}{{\text{m}}^2}$.
Note – In these kind of questions, we should know what Pythagoras theorem i.e. ${h^2} = {b^2} + {p^2}$ .Also, we should know what are the formulas for circle and triangle i.e. area of circle$ = \pi {r^2}$ and area of triangle$ = \dfrac{1}{2} \times base \times height$ and their properties i.e. the line from the center of the circle to the point on the tangent of the circle where it touches the circle is always perpendicular to each other.
One must remember all these concepts and formulas to avoid the common mistakes like which is to be taken hypotenuse, base and perpendicular and the sides of the triangle are assumed as tangents to incircle. Also, one must do remember this method as it is the only approach to find the area of the shaded region.
Recently Updated Pages
Which is the Longest Railway Platform in the world?

India Manned Space Mission Launch Target Month and Year 2025 Update

Which of the following pairs is correct?

The Turko-Afghan rule in India lasted for about?

In which state Jews are not considered minors?

What is Ornithophobia?

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

The draft of the Preamble of the Indian Constitution class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

How many members did the Constituent Assembly of India class 10 social science CBSE

Write an application to the principal requesting five class 10 english CBSE

The Constitution of India was adopted on A 26 November class 10 social science CBSE




