Question

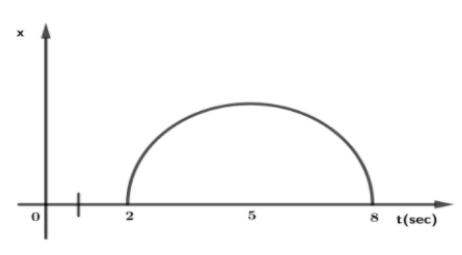
In Given figure, the position-time graph is shown, which is semicircle from \[t = 2\] to $t = 8$ sec. Find time $t$ at which the instantaneous velocity is equal to average velocity over first $t$ seconds.

Answer 1

Hint: Instantaneous velocity is velocity of an object at particular instant of time whereas, average velocity is total displacement covered in total time. In the given diagram We will use the slope on the given curve at a point as the velocity measurement as velocity $ = \dfrac{\text{displacement(x)}}{\text{time(s)}}$.

Complete step by step answer:
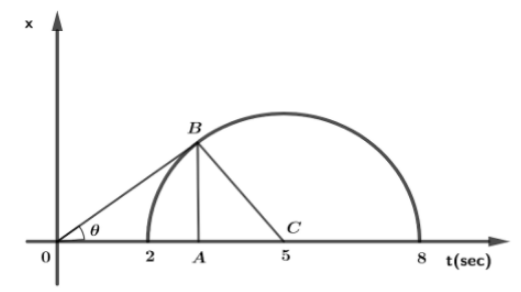
Let us first draw the diagram and consider a point $B$ on the curve and we assume that at this point B, instantaneous velocity is equal to the average velocity. Draw a line tangent from initial point $O$ origin to point $B$. Draw perpendicular from point $B$ to point $A$. Now, From the diagram we need to find $AO$ which is the time at which instantaneous velocity is equal to average velocity.

Since CB is the radius of semicircle whose length is $ = 3\,unit.$
$OC = 5\,unit$. We know, Tangent $OB$ is perpendicular to radius $BC$ so ,
Using Pythagoras theorem in the right-angled triangle $OBC$.
We have, ${(OC)^2} = {(OB)^2} + {(BC)^2}$
${(OB)^2} = 25 - 9$
${(OB)^2} = 16$
$OB = 4\,unit$

Now, In right angle triangle OAB,
$\cos \theta = \dfrac{{OA}}{{OB}}$
$\Rightarrow \cos \theta = \dfrac{{OA}}{4}$ $ \to (i)$
Now, In right angle triangle OBC,
$\cos \theta = \dfrac{{OB}}{{OC}}$
$\Rightarrow \cos \theta = \dfrac{4}{5}$ $ \to (ii)$
Now, Comparing both equations (i) and (ii) we get,
$\dfrac{{OA}}{4} = \dfrac{4}{5}$
$\Rightarrow OA = \dfrac{{16}}{5}$
$\therefore OA = 3.2\sec $
Since, from the diagram we know OA is the time from starting when instantaneous velocity equals to average velocity.

Hence, the time(t) at which both velocity became equals is $ = 3.2\sec $.

Note:In a position-time graph the slope at a point on a path curve is equals to its velocity and Instantaneous velocity of a body would be equal to average velocity when slope of line joining final and initial point will be same as slope of that point on curve.