Question

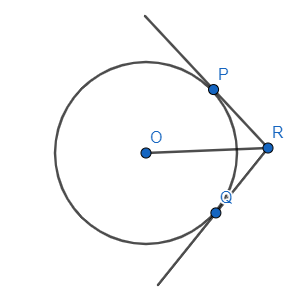
In figure, two tangents $RQ$ and $RP$ are drawn from an external point $R$ to the circle with center $O$. If $\angle PRQ={{120}^{\circ }}$, then prove that $OR=PR+RQ$

Answer 1

Hint: In this question we have been told to prove that the line segment $OR=PR+RQ$. We will first join the points $OP$ and $OQ$. On joining we will get two triangles which we will prove congruent. We will then value $\angle PRQ={{120}^{\circ }}$and use this in the trigonometric identity of cosine and substitute the value to prove the given statement.

Complete step by step solution:
We have been given that we have to prove that $OR=PR+RQ$.
On joining the points $OP$ and $RQ$ in the given figure, we get:

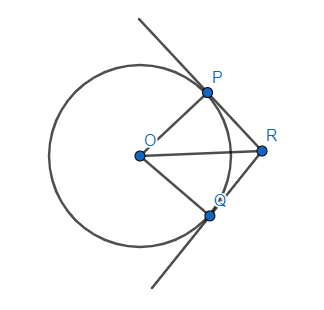
Now on joining the points we have two triangles which are $\Delta POR$ and $\Delta QOR$.
Now in $\Delta POR$ and $\Delta QOR$, we can see that:
$OP=OR$ , which is the radius of the circle hence it will be the same.
$RP=RQ$, tangents from the external point are the same.
$OR=OR$, which is the same side shared by both the triangles.
Therefore by $SSS$ congruence, $\Delta POR\cong \Delta QOR$
Now by using C.P.C.T which means corresponding part of congruent triangles, we can say that:
$\Rightarrow \angle PRO=\angle QRO\to \left( 1 \right)$
Now we can see that:
$\Rightarrow \angle PRQ=\angle PRO+\angle QRO$
Now we know that $\angle PRQ={{120}^{\circ }}$therefore, on substituting, we get:
$\Rightarrow {{120}^{\circ }}=\angle PRO+\angle QRO\to \left( 2 \right)$
Now since $\angle PRO=\angle QRO$, they will have an equal angle which will be ${{60}^{\circ }}$, since ${{60}^{\circ }}+{{60}^{\circ }}={{120}^{\circ }}$
On substituting the value of $\angle QRO=\angle PRO$ in equation $\left( 2 \right)$, we get:
$\Rightarrow {{120}^{\circ }}=\angle PRO+\angle PRO$
On simplifying, we get:
$\Rightarrow {{120}^{\circ }}=2\angle PRO$
On dividing both the sides by $2$, we get:
$\Rightarrow \angle PRO={{60}^{\circ }}$
Now in $\Delta POR$
$\Rightarrow \cos {{60}^{\circ }}=\dfrac{PR}{OR}$
We know the value of $\cos {{60}^{\circ }}=\dfrac{1}{2}$, therefore on substituting, we get:
$\Rightarrow \dfrac{1}{2}=\dfrac{PR}{OR}$
On cross multiplying, we get:
$\Rightarrow OR=2PR$
It can be written as:
$\Rightarrow OR=PR+PR$
And since $RQ=PR$, on substituting, we get:
$\Rightarrow OR=PR+RQ$, hence proved.

Note: In this question we have used the trigonometric identity of cosine. It is to be remembered that which gives us the length of the adjacent side divided by the length of the hypotenuse. The values of $\cos \theta $ at various angles should be remembered and substituted wherever necessary. It is also to be remembered that the property C.P.C.T can only be used if the triangles are congruent.