Question

In figure two chords AB and CD of a circle intersect each other at the point P (when produced) outside the circle. Prove that:
1) $\Delta PAC \sim \Delta PDB$
2) $PA.PB = PC.PD$

Answer 1

Hint: As ABCD is the cyclic quadrilateral and we know the cyclic quadrilateral exterior angle is equal to the opposite interior angle and that means $\angle PAC = \angle PDB$. So now use the similarity properties as both has angle P in common in both $\Delta PDB\,\& \,\,\Delta PAC$.

Complete step-by-step answer:
In the question two chords are given AB and CD which when produced further intersect at P
So lets show in diagram

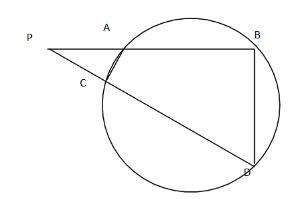
Here ABCD forms a cyclic quadrilateral whose every point lies on a circle. So it is cyclic.
And we know that in cyclic quadrilateral
1) Sum of opposite angles is equal to $180$
i.e. $\angle BAC + \angle BDC = 180$ and $\angle ABD + \angle ACD = 180$
2) And also the exterior angle is equal to the opposite interior angle.
i.e. $\angle PAC = \angle BDC\,\,\,\,\,\& \,\,\,\,\angle PCA = \angle DBA$
Now we need to prove that $\Delta PAC$ is similar to \[\Delta PDB\]
So as we can see that ABCD is cyclic quadrilateral. So,
$\angle CDB = \angle PAC\,\,\,\,\,\,\,\, \to \left( 1 \right)$
As $\angle PAC$ is the exterior angle and $\angle CDB$ is the opposite interior angle
So in $\Delta PDB\,\,\,\& \,\,\Delta PAC$
We know that angle P is common in both. So,
$\angle P = \angle P$
And $\angle CDB = \angle PAC$ (proved earlier)
So by AA property
$\Delta PAC \sim \Delta PDB$
As we proved that both triangle are similar therefore, its sides are also in proportion that means ratio of sides are equal
$\dfrac{{PA}}{{PC}} = \dfrac{{PD}}{{PB}}$
So on cross multiplying
$PA.PB = PD.PC$
Hence proved.

Note: We don’t need to check all the angles as because if two angles are equal then the third one will automatically be equal in a triangle. If two angles are equal then we can say that both triangles are similar triangles.