Question

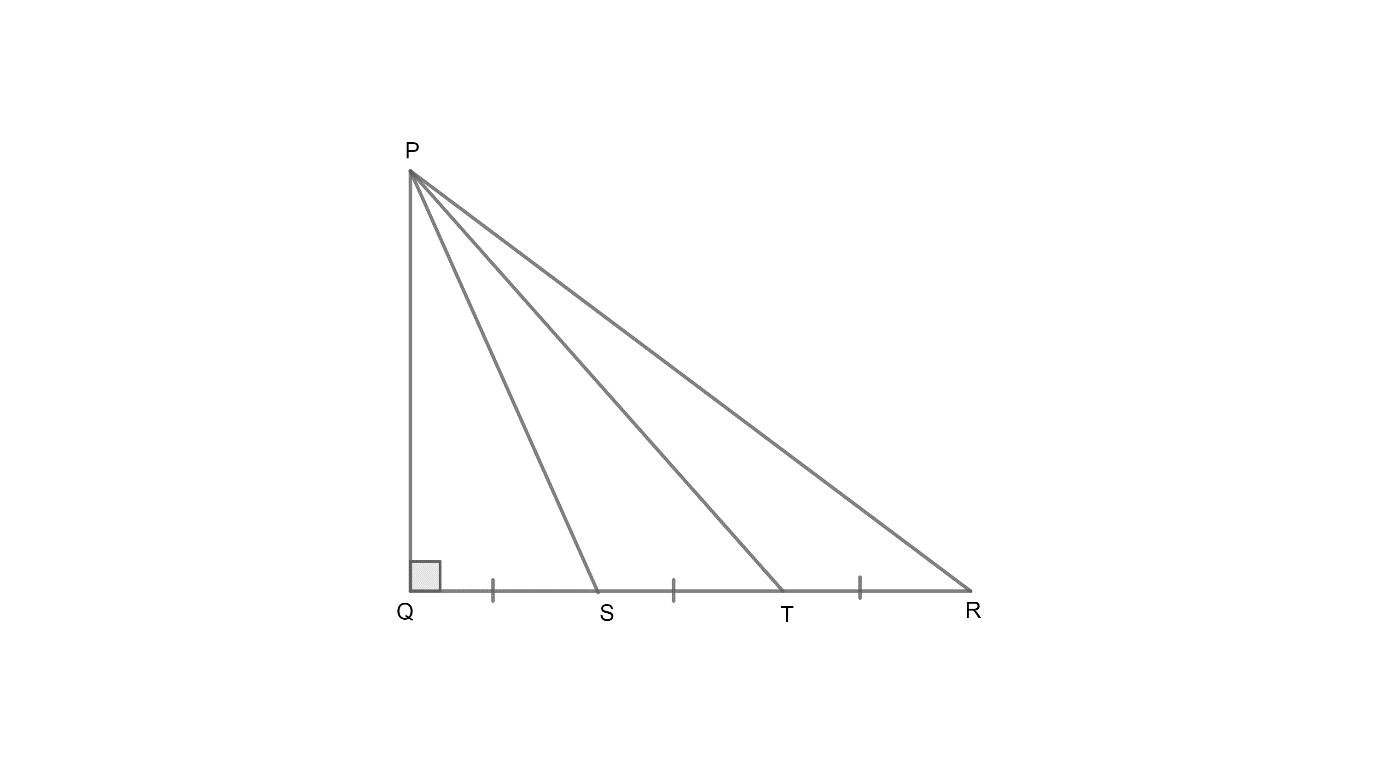
In figure, S and T trisect the side QR of a triangle PQR. Then $8P{{R}^{2}}=2P{{R}^{2}}+9P{{S}^{2}}$. State whether the above statement is true or false.

A. True
B. False

Answer 1

Hint: We will use the fact given to us that S and T trisect QR. We will first apply Pythagoras Theorem in $\Delta PQR$. Then in $\Delta PTQ$ and finally in $\Delta PSQ$, then we will use these three equations to prove the given equation.

Complete step-by-step answer:
Now, we have been given that S and T trisect the side QR of a right triangle PQR.

So, we have,
$\begin{align}
  & QS=ST=TR.........\left( 1 \right) \\
 & QT=2QS........\left( 2 \right) \\
 & QR=3QS.........\left( 3 \right) \\
\end{align}$
Now, we will apply the Pythagoras Theorem in $\Delta PQR$. So, we have,
$P{{R}^{2}}=P{{Q}^{2}}+Q{{R}^{2}}$
Now, from (3) we have,
$\begin{align}
  & P{{R}^{2}}=P{{Q}^{2}}+{{\left( 3QS \right)}^{2}} \\
 & P{{R}^{2}}=P{{Q}^{2}}+9Q{{S}^{2}} \\
\end{align}$
Now, multiplying both sides by 3 we have,
$3P{{R}^{2}}=3P{{Q}^{2}}+27Q{{S}^{2}}...........\left( 4 \right)$
Now, we will apply Pythagoras in $\Delta PTQ$. So, we have,
$P{{T}^{2}}=P{{Q}^{2}}+Q{{T}^{2}}$
Now, from (2) we have,
$\begin{align}
  & P{{T}^{2}}=P{{Q}^{2}}+{{\left( 2QS \right)}^{2}} \\
 & P{{T}^{2}}=P{{Q}^{2}}+4Q{{S}^{2}} \\
\end{align}$
Multiplying both side by 8 we have,
$8P{{T}^{2}}=8P{{Q}^{2}}+32Q{{S}^{2}}...........\left( 5 \right)$
Now, we will apply Pythagoras in $\Delta PQS$. So, we have,
$P{{S}^{2}}=P{{Q}^{2}}+Q{{S}^{2}}$
Now, we multiply both sides by 5. So, we have,
$5P{{S}^{2}}=5P{{Q}^{2}}+5Q{{S}^{2}}...........\left( 6 \right)$
Now, adding (4) and (6) we have,
$5P{{S}^{2}}+3P{{R}^{2}}=8P{{Q}^{2}}+32Q{{S}^{2}}$
Now, equating with (5), we have,
$8P{{T}^{2}}=5P{{S}^{2}}+3P{{R}^{2}}$
Hence, the statement is true and the correct option is (B).

Note: It is important to note that we have used a fact that if a $\Delta ABC$ is $90{}^\circ $ at B. Then we have $A{{C}^{2}}=A{{B}^{2}}+B{{C}^{2}}$ also, it is important to note that we have converted QR, QT in terms of QS and then multiplied the equation with the constant as per the given equation to find the answer.