Question

In figure, \[OQ:PQ = 3:4\] and the perimeter of \[\Delta POQ = 60cm\]. Determine PQ, QR and OP.

Answer 1

Hint: First we will assume the common ratio to be x then will find the sides of the triangle using the Pythagoras theorem in terms of x and since the perimeter of the triangle is given , we will put in the values of sides in the formula of perimeter and find the value of x. Then substitute the value of x in each of the sides to get their values.
The Pythagoras formula is given by:-
\[{\left( {{\text{hypotenuse}}} \right)^2} = {\left( {{\text{base}}} \right)^{\text{2}}}{\text{ + }}{\left( {{\text{perpendicular}}} \right)^2}\]

Complete step-by-step answer:

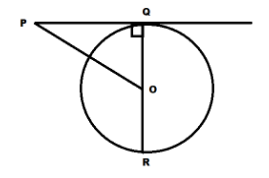
Let the common ratio be x then,
\[
  OQ = 3x................\left( 1 \right) \\
  PQ = 4x.................\left( 2 \right) \\
 \] \[\]
Since , \[\;\Delta POQ\] is a right angled triangle therefore we will apply Pythagoras formula in this triangle to get the length of \[OP\] in terms of x.
Since, the right angle is at vertex Q therefore,
\[
  {\text{hypotenuse}} = OP \\
  {\text{base}} = OQ \\
  {\text{perpendicular}} = PQ \\
 \]
Applying Pythagoras formula we get:-
\[
  {\left( {{\text{hypotenuse}}} \right)^2} = {\left( {{\text{base}}} \right)^{\text{2}}}{\text{ + }}{\left( {{\text{perpendicular}}} \right)^2} \\
  {\left( {OP} \right)^2} = {\left( {OQ} \right)^2} + {\left( {PQ} \right)^2} \\
 \]
Putting in the value of \[PQ\] and \[OQ\] we get:-
\[
  {\left( {OP} \right)^2} = {\left( {3x} \right)^2} + {\left( {4x} \right)^2} \\
  {\left( {OP} \right)^2} = 9{x^2} + 16{x^2} \\
 \]
Simplifying it further we get:-
\[
  {\left( {OP} \right)^2} = 9{x^2} + 16{x^2} \\
  {\left( {OP} \right)^2} = 25{x^2} \\
 \]
Now taking square root both the sides:-
\[
  OP = \sqrt {25{x^2}} \\
   \Rightarrow OP = 5x................\left( 3 \right) \\
 \]
Now since the perimeter of the triangle is 60 cm and is equal to the sum of all sides therefore,
\[
  3x + 4x + 5x = 60 \\
  12x = 60 \\
   \Rightarrow x = \dfrac{{60}}{{12}} \\
   \Rightarrow x = 5 \\
 \]
Putting the value of x in equations 1 ,2 and 3 we get:-
\[
  OP = 5x \\
  OP = 5\left( 5 \right) \\
  OP = 25cm \\
  OQ = 3x \\
  OQ = 3\left( 5 \right) \\
  OQ = 15cm \\
  PQ = 4x \\
  PQ = 4\left( 5 \right) \\
  PQ = 20cm \\
 \]
Now since QR is the diameter of the circle and OQ is the radius of the circle and since,
\[{\text{diameter = 2}}\left( {{\text{radius}}} \right)\]
Therefore,
\[QR = 2\left( {OQ} \right)\]
Putting the known value we get:-
\[
  QR = 2\left( {15} \right) \\
  QR = 30cm \\
 \]
Hence, \[PQ = 20cm\], \[QR = 30cm\] and \[OP = 25cm\].

Note: In a right angled triangle, the longest side is hypotenuse and the sides containing the right angle are the base and the perpendicular.
Also the perimeter of any polygon is the sum of all the sides of the polygon.