Question

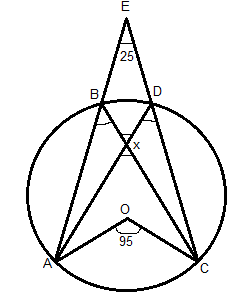
In figure, O is the center, then ∠BXD =

$
  {\text{A}}{\text{. 65}}^\circ \\
  {\text{B}}{\text{. 60}}^\circ \\
  {\text{C}}{\text{. 70}}^\circ \\
  {\text{B}}{\text{. 55}}^\circ \\
$

Answer 1

Hint: In order to find the ∠BXD, we use the properties of angles of triangle inscribed inside a circle, i.e. the concepts of half angle, angles on a straight line and angle in a quadrilateral.

Complete Step-by-Step solution:
Given Data,
∠AOC = 95° and ∠BED = 25°

From the figure, the angles ∠ABC and ∠ADC are said to be half angles to ∠AOC, if they are aligned in such a way.

⟹Hence, ∠ABC = ∠ADC = \[\dfrac{{95^\circ }}{2}\] (Half Angle)

Now, we also know sum of angles on a straight line is 180°, i.e. from the figure ∠ABC + ∠EBX = 180°, i.e.
∠EBX = 180° - \[\dfrac{{95^\circ }}{2}\] ​= $\dfrac{{265^\circ }}{2}$

In quadrilateral BEXD, we know
Sum of all the angles in a quadrilateral is 360°, hence

∠BED + ∠EBX + ∠BXD + ∠XDE = 360°
⟹25° + $\dfrac{{265^\circ }}{2}$ + ∠BXD + $\dfrac{{265^\circ }}{2}$ = 360°
⟹∠BXD = 360°- 265° - 25°
⟹∠BXD = 70°

Note: In order to solve problems of this type the key is to have adequate knowledge in properties of triangles and the concepts of angles of triangle inscribed in a circle, i.e. half angle etc. We also use the concept of angles on a straight line and angles in a quadrilateral.