Question

In figure, find the area of the shaded region. (Use π = 3.14)

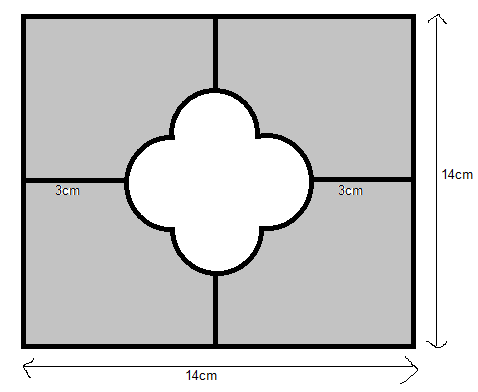
Answer 1

Hint: To find the area of the shaded region we compute the total area of the square and subtract the area of the unshaded region from it. The unshaded region can be divided into a square and 4 semi-circles.

Complete step-by-step answer:

It is impossible to compute the area of an unshaded region with the given data as we do not know the formula of the area of that shape.
So to find the area of unshaded region, we divide it into a square in the middle and 4 semi-circles around it, which looks like the figure below

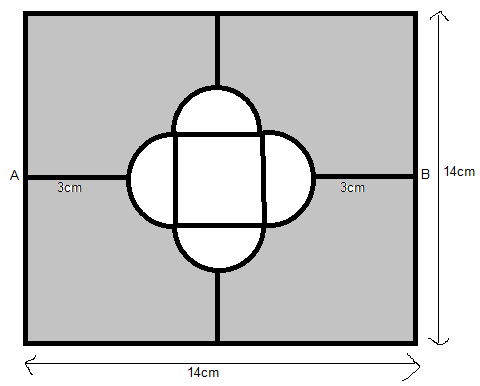
From the figure if we observe the line segment from A to B = 14 cm.
AB = 3 + 3 + 2(diameter D of the circle)
      = 6 + 2(2r)
14 = 6 + 4r
Hence radius of the semi-circle (r) = 2cm.
Now, AB can also be written as AB = 3 + 3 + r + r + a (side of the inside square)
⟹14 = 6 + 2 + 2 + a
Therefore the side of the inner square = 4cm.
Now, area of the whole big square whose side is 14cm is ${{\text{s}}^2}$= ${\left( {14} \right)^2} = 196{\text{c}}{{\text{m}}^2}$
Area of small inside square whose side is 4cm is ${{\text{a}}^2} = {4^2} = 16{\text{c}}{{\text{m}}^2}$
Area of 4 semi-circles is A = $4 \times \dfrac{{\pi {{\text{r}}^2}}}{2} = 4 \times \dfrac{{3.14 \times {2^2}}}{2} = 25.12{\text{c}}{{\text{m}}^2}$
Now, area of shaded region = area of big whole square – area of small inner square – area of 4 semi-circles.
⟹Area of shaded region = 196 – 16 – 25.12 = 154.88${\text{c}}{{\text{m}}^2}$.

Note: In order to solve this type of question the key is to divide the unshaded region into known shapes and then we compute its area. We then subtract this from the total area to find the area of the unshaded part.
Area of square with side a = ${{\text{a}}^2}$
Area of a semicircle with radius r =$\dfrac{{\pi {{\text{r}}^2}}}{2}$.