Question

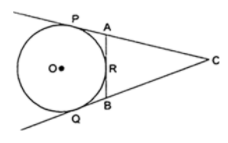
In figure, CP and CQ are tangents to the circle with center O. ARB is another tangent touching the circle at R. If CP = 12 cm, and BC = 8 cm, then find the length of BR.

Answer 1

Hint: Read the question carefully, and consider all the given information as it leads to solution.
Tangent to a circle is a line that intersects the circle at only one point.
The property of Pair of tangents to a circle drawn from an external point is the key to solve this question.

Complete step by step solution:
Step 1: Draw the labeled diagram carefully:

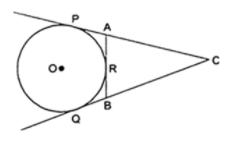
   Figure 1: circle with center O
Step 2: Given that:
Line CP, CQ, and AB are tangents to the circle with center O.
Length CP = 12 cm, BC = 8 cm
Step 3: State the theorem related to Pair of tangents to a circle drawn from an external point:
Theorem 1: The lengths of tangents drawn from an external point to a circle are equal.

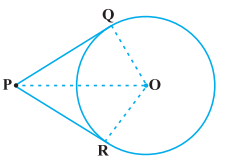
      Figure 2: tangents PQ and PR to the circle with center O
Hence, length PQ = length PR
Step 4: apply the theorem
Here, line CP and CQ are tangents from external point C to the circle with center O.
$ \Rightarrow $CP = CQ
Hence, CQ = 12 cm
Step 5: since, QBC is a straight line:
 Therefore, CQ = BQ + BC
                            12 = BQ + 8
                       BQ = 12 – 8
                      $ \Rightarrow $BQ = 4 cm. …… (1)
Step 6: apply the theorem
Here, line BQ and BR are tangents from external point B to the circle with center O.
$ \Rightarrow $BQ = BR
Hence, BR = 4 cm (from (1))

Therefore, the required length of the BR is 4 cm.

Note:
Another important theorem of tangents and circle:
 Theorem: The tangent at any point of a circle is perpendicular to the radius through the point of contact.

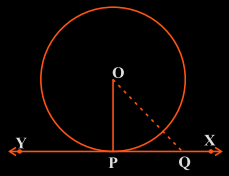
    Figure 3: tangent XY to the circle with center O.
Hence, $OP \bot PQ$
There is only one tangent at a point of the circle.