Question

In figure below, segment MN is a chord of a circle with centre O. MN=25, L is a point on chord MN such that ML=9 and $ d\left( {O,L} \right) = 5 $ . Find the radius of the circle.

Answer 1

Hint: MN is the chord of the circle with centre O. So first draw a perpendicular line from centre O to the chord. A line drawn from centre perpendicular to the chord bisects the chord. Say the perpendicular line met the chord at X. Find the length of XL and using XL find the length of XN and using XN find the Length of ON which is the required radius.

Complete step-by-step answer:
We are given that in a circle, segment MN is a chord with centre O, MN=25, L is a point on the chord MN such that ML=9 units and $ d\left( {O,L} \right) = 5 $ .
We are first drawing a diagram according to the given measurements.

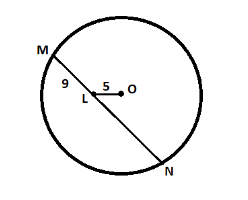
Let us first draw a perpendicular line from the centre O to the chord MN and this perpendicular line touches the chord MN at X.

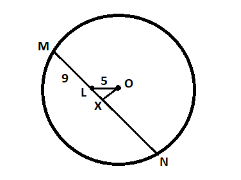
We know that a perpendicular line drawn from the centre of a circle to its chord bisects the chord. This means that the line OX bisects the chord MN.
This gives that the length of MX is equal to length of XN, $ MX = XN $
We already know that the length of the chord MN is 25, this means the length of $ MX = XN = \dfrac{{25}}{2} = 12.5 $
As we can see $ ML + LX = MX = 12.5 $
We know the length of ML is 9.
Therefore, $ 9 + LX = 12.5 \Rightarrow LX = 12.5 - 9 = 3.5 $
The obtained length of LX is 3.5.
As we can see the triangle OLX is a right angled triangle with right angle at X.
So by Pythagoras theorem, $ O{L^2} = O{X^2} + L{X^2} $
OL is 5 and LX is 3.5
 $ {5^2} = O{X^2} + {3.5^2} \Rightarrow O{X^2} = 25 - 12.25 = 12.75 $ …….. equation (1)

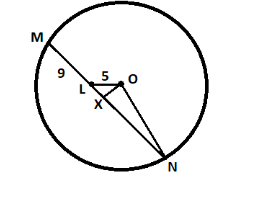
As we can see, triangle OXN is also a right triangle and the right angle is at X.
So by Pythagoras theorem, $ O{N^2} = O{X^2} + X{N^2} $
We already know that the length of XN is 12.5 units and from equation we can get the square of OX
 $ O{N^2} = 12.75 + {\left( {12.5} \right)^2} $
 $ \Rightarrow O{N^2} = 12.75 + 156.25 = 169 $
 $ \therefore ON = \sqrt {169} = 13 $
ON is the radius, so the radius of the given circle is 13 units.
So, the correct answer is “13 units”.

Note: Length is a measurement, so for every length value we should not forget to write its units. If no units are given then the word ‘units’ must be written after the values. A chord is a secant with endpoints on the circle. The longest chord in a circle is its diameter. Pythagoras theorem can be used only in right triangles.