Question

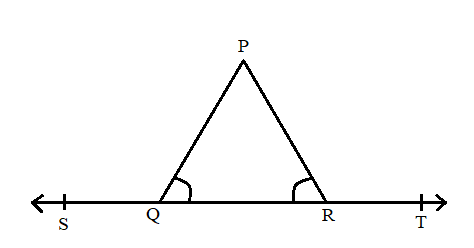
In figure \[\angle PQR = \angle PRQ\], then prove that \[\angle PQS = \angle PRT\].

Answer 1

Hint: Here we are asked to verify the given two angles are equal by using the given data. For that, we will first name the given angles. When a straight line is divided into two by a ray or line then the sum of those two angles will be equal to \[180^\circ \]. Since the given angles and the required angles are in this form using this property, we will find the required angles.

Complete step-by-step solution:
It is given that the angles \[\angle PQR\] and \[\angle PRQ\] are equal in the given diagram. We aim to verify that the angles \[\angle PQS\] and \[\angle PRT\] are equal.
Let us consider the angle \[\angle PQR\] be \[x^\circ \]. It is given that \[\angle PQR = \angle PRQ\] therefore, the angle \[\angle PRQ\] will also be equal to \[x^\circ \]. Here we are aiming to verify that \[\angle PQS = \angle PRT\]. For that, we first need to find those angles then by comparing them we will be able to verify the given condition.
We know that when a ray or a line cuts the straight line into two then the sum of those angles will be equal to one hundred and eighty degrees.
Here we can see that a line \[QP\] cuts the straight line \[ST\] into two which makes two angles \[\angle PQR\] and \[\angle PQS\]. So, we can say that \[\angle PQR + \angle PQS = 180^\circ \]. We have that \[\angle PQR = x\] substituting this we get \[x + \angle PQS = 180^\circ \]. Since we need the measure of the angle \[\angle PQS\] , let's take the degree \[x^\circ \] to the other side.
\[\angle PQS = 180^\circ - x^\circ \]…………….\[\left( 1 \right)\]
Also, from the diagram, we can see that a line \[RP\] cuts the straight line \[ST\] into two which makes two angles \[\angle PRQ\] and \[\angle PRT\]. So, we can say that \[\angle PRQ + \angle PRT = 180^\circ \]. We have that \[\angle PRQ = x\] substituting this we get \[x + \angle PRT = 180^\circ \]. Since we need the measure of the angle \[\angle PRT\] , let's take the degree \[x^\circ \] to the other side.
\[\angle PRT = 180^\circ - x^\circ \]……………..\[\left( 2 \right)\]

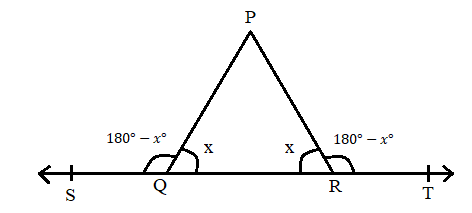
Thus, from the equation \[\left( 1 \right)\] and \[\left( 2 \right)\] we get that \[\angle PQS = \angle PRT\].
Therefore, we verified the given condition that the angles \[\angle PQS\] and \[\angle PRT\] are equal.

Note: In mathematics, under the topic lines and angles we have that when a line or a ray cuts a straight line into two then the sum of the angles formed will be equal to \[180^\circ \]. This can also be known as supplementary angles, that is, when the sum of two angles is equal to \[180^\circ \] then they are called supplementary angles.