Question

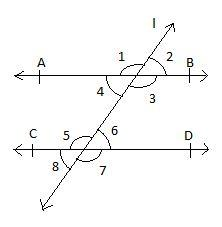
In figure, $AB\parallel CD$ and $\angle 1$ and $\angle 2$ are in the ratio 3:2. Determine all angles from 1 to 8.

Answer 1

Hint: Assume angles 1 and 2 as 3x and 2x respectively. Take the sum of these angles equal to 180 degrees, because they are linear pairs. Find the value of x and substitute it in the assumed value of angle 1 and 2. Once angles 1 and 2 are obtained, substitute $\angle 1=\angle 3,\angle 2=\angle 4$ because they are vertically opposite angles and $\angle 1=\angle 5,\angle 2=\angle 6$ because they are corresponding angles. Similarly, $\angle 7=\angle 5$ and $\angle 8=\angle 6$, as they are vertically opposite angles.

Complete step-by-step answer:
We have been given that: $\angle 1$ and $\angle 2$ are in the ratio 3:2. So, let us assume that angle 1 is 3x and angle 2 is 2x degrees.

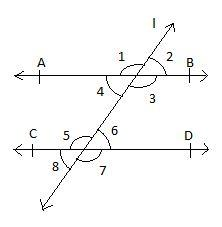
Clearly, we can see that angle 1 and angle 2 are linear pair, that means, the measure of sum of these angles is 180 degrees. Therefore,
\[\begin{align}
  & \angle 1+\angle 2={{180}^{\circ }} \\
 & \Rightarrow 3x+2x={{180}^{\circ }} \\
 & \Rightarrow 5x={{180}^{\circ }} \\
\end{align}\]
Dividing both sides by 5 we get,
$\begin{align}
  & x=\dfrac{{{180}^{\circ }}}{5} \\
 & \Rightarrow x={{36}^{\circ }} \\
\end{align}$
Therefore, the measure of angle 1 and 2 are:
\[\begin{align}
  & \angle 1=3x=3\times {{36}^{\circ }}={{108}^{\circ }} \\
 & \angle 2=2x=2\times {{36}^{\circ }}={{72}^{\circ }} \\
\end{align}\]
Now, we know that pairs of vertically opposite angles and pairs of corresponding angles are equal. Here, as we can see that, angle 1 and angle 3 are vertically opposite angles, therefore,
$\angle 3=\angle 1={{108}^{\circ }}$
Similarly, $\angle 4=\angle 2={{72}^{\circ }}$.
Now, angle 1 and 5 are corresponding angles, therefore,
$\angle 5=\angle 1={{108}^{\circ }}$
Similarly, $\angle 6=\angle 2={{72}^{\circ }}$.
To determine angles 7 and 8, we have to use the concept of vertically opposite angles once more, therefore,
$\angle 7=\angle 5={{108}^{\circ }}$
And, $\angle 8=\angle 6={{72}^{\circ }}$
So, all the angles are:
$\angle 1=\angle 3=\angle 5=\angle 7={{108}^{\circ }}$
$\angle 2=\angle 4=\angle 6=\angle 8={{72}^{\circ }}$

Note: We can also use the concept of alternate angles. We know that the pair of alternate angles are equal. Here, in the above figure, angle 1 and 7 are one of the pairs of alternate angles. Similarly angle 2 and 8 are also the pair of alternate angles. Properties of sum of adjacent angles equal to 180 degrees, can also be used. For example: $\angle 4+\angle 5={{180}^{\circ }}$. But, remember that first we have to calculate the value of ‘x’.