
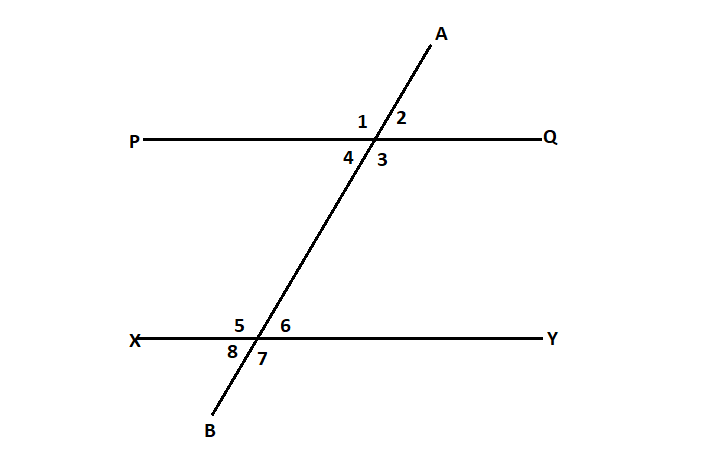
In fig, PQ||XY and $\angle 1 = {110^0},\angle 8 = {70^0}$, Then find $\angle 3$ and $\angle 6$
A. $\angle 3 = {60^0}$, $\angle 6 = {120^0}$
B. $\angle 3 = {110^0}$, $\angle 6 = {70^0}$
C. $\angle 3 = {100^0}$, $\angle 6 = {80^0}$
D. $\angle 3 = {90^0}$, $\angle 6 = {90^0}$

Answer
554.1k+ views
Hint: According to the question we have to find $\angle 3$ and $\angle 6$ when PQ||XY and $\angle 1 = {110^0},\angle 8 = {70^0}$. According to fig PQ||XY and AB is a transversal line which is cutting a pair of two parallel lines PQ and XY as mentioned above in the figure.
Now we have to use the transversal rule for both of the lines PQ and XY, Where vertically opposite angles are equal to each other.
As in above figure the vertically opposite angles for line PQ are $\angle 1,\angle 3$ and $\angle 2,\angle 4$ similar vertically opposite angles for line XY are $\angle 5,\angle 7$ and $\angle 6,\angle 8$
Complete step by step answer:
Step 1: First of all as mentioned in the question above PQ||XY and $\angle 1 = {110^0}$ So, $\angle 1$ and $\angle 3$ will be vertically opposite angles we can also understand with the help of the diagram mention below,

$ \Rightarrow \angle 1 = \angle 3$……………………………….(1)
Step 2: Now as we know that $\angle 1 = {110^0}$ hence on substituting in the expression (1),
$
\Rightarrow \angle 1 = \angle 3 \\
\Rightarrow \angle 3 = {110^0} \\
$
Step 3: Now, as mentioned in the question above PQ||XY and $\angle 8 = {70^0}$ So, $\angle 6$ and $\angle 8$ will be vertically opposite angles we can also understand with the help of the diagram mention below,
$ \Rightarrow \angle 6 = \angle 8$……………………………….(2)
Step 4: Now as we know that $\angle 8 = {70^0}$ hence on substituting in the expression (2),
$
\Rightarrow \angle 6 = \angle 8 \\
\Rightarrow \angle 6 = {70^0} \\
$
Hence, we have obtained the $\angle 3 = {110^0}$ and $\angle 6 = {70^0}$ with the help of vertically opposite angles rule. Therefore option (B) is correct.
Note: When two lines intersect they form two pairs of opposite angles and vertical angles are always congruent, which means that they are equal to each other.
To angles are said to be supplementary angles when the sum of two angles is ${180^0}$
Now we have to use the transversal rule for both of the lines PQ and XY, Where vertically opposite angles are equal to each other.
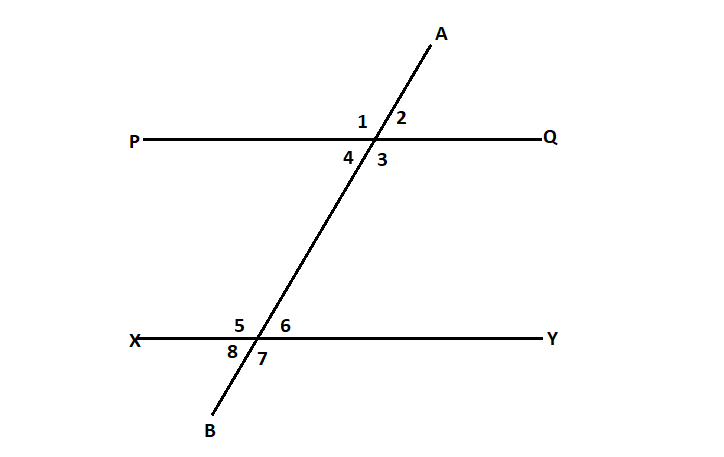
As in above figure the vertically opposite angles for line PQ are $\angle 1,\angle 3$ and $\angle 2,\angle 4$ similar vertically opposite angles for line XY are $\angle 5,\angle 7$ and $\angle 6,\angle 8$
Complete step by step answer:
Step 1: First of all as mentioned in the question above PQ||XY and $\angle 1 = {110^0}$ So, $\angle 1$ and $\angle 3$ will be vertically opposite angles we can also understand with the help of the diagram mention below,

$ \Rightarrow \angle 1 = \angle 3$……………………………….(1)
Step 2: Now as we know that $\angle 1 = {110^0}$ hence on substituting in the expression (1),
$
\Rightarrow \angle 1 = \angle 3 \\
\Rightarrow \angle 3 = {110^0} \\
$
Step 3: Now, as mentioned in the question above PQ||XY and $\angle 8 = {70^0}$ So, $\angle 6$ and $\angle 8$ will be vertically opposite angles we can also understand with the help of the diagram mention below,

$ \Rightarrow \angle 6 = \angle 8$……………………………….(2)
Step 4: Now as we know that $\angle 8 = {70^0}$ hence on substituting in the expression (2),
$
\Rightarrow \angle 6 = \angle 8 \\
\Rightarrow \angle 6 = {70^0} \\
$
Hence, we have obtained the $\angle 3 = {110^0}$ and $\angle 6 = {70^0}$ with the help of vertically opposite angles rule. Therefore option (B) is correct.
Note: When two lines intersect they form two pairs of opposite angles and vertical angles are always congruent, which means that they are equal to each other.
To angles are said to be supplementary angles when the sum of two angles is ${180^0}$
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Social Science: Engaging Questions & Answers for Success

Master Class 11 Biology: Engaging Questions & Answers for Success

Class 11 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE




