Question

In Fig., line $n$ is a transversal to lines $l$ and $m$ . Identify the following: Alternate and corresponding angles in Fig.

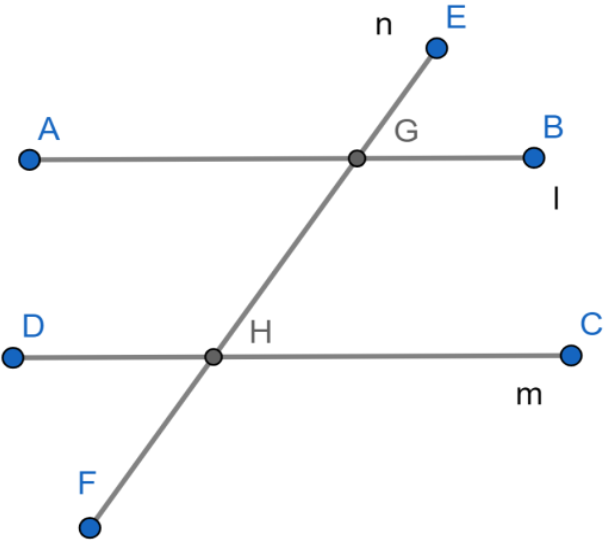
Answer 1

Hint: For answering this question we will use the definitions of the corresponding and alternate interior and exterior angles which are as follows for the case of transversal the angles which are on the matching corners of the two lines are corresponding and the pair of angles on the inner side of the two lines and opposite sides of the transversal are called alternate interior angles.

Complete step-by-step solution:
Now for answering this question we need to be crystal clear with the concept like the corresponding angles and alternate interior angles and alternate exterior angles.
Alternate interior angles are defined as a pair of angles on the inner side of each of the two lines that cross each other such as in the case of transversal but on opposite sides.
Alternate exterior angles are defined as a pair of angles on the outer side of each of the two lines that cross each other such as in the case of transversal but on opposite sides.
Corresponding angles are defined as a pair of angles present in the matching corners of the two lines crossing each other by another line similar to in the case of the transversal.
 

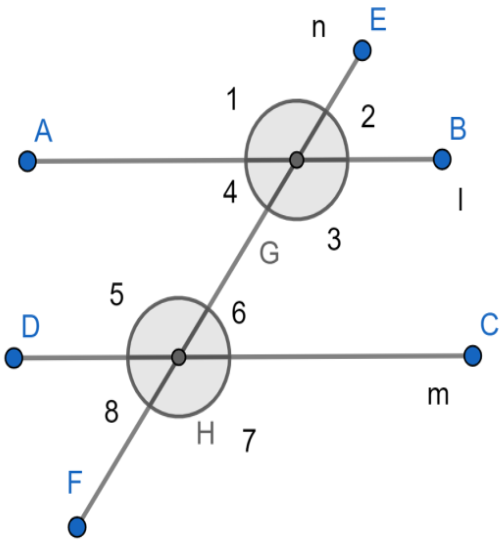
Hence here $1,5$ and $2,6$ and $3,7$ and $4,8$ are the $4$ pairs of corresponding angles.
Similarly from the definition here $4,6$ and $3,5$ are $2$ pairs of alternate interior angles.
Similarly here $2,8$ and $1,7$ are $2$ pairs of alternate exterior angles.

Note: Here while answering questions of this type using this concept we can obtain an important point the pair of corresponding angles are equal and the pair of sum of alternate exterior angles is ${{180}^{\circ }}$ and similarly the sum of pair of alternate interior angles is also ${{180}^{\circ }}$ . So we can say that \[1=5\text{ }and\text{ }2=6\text{ }and\text{ }3=7\text{ }and\text{ }4=8\] and \[4+6=3+5={{180}^{\circ }}\] and \[2+8=1+7={{180}^{\circ }}\] . So as we know that the vertically opposite angles are equal so \[1=3\text{ }and\text{ }2=4\text{ }and\text{ }7=5\text{ }and\text{ }8=6\] and that the sum of the linear pair of angles is ${{180}^{\circ }}$ that is \[1+2=3+4=5+6=7+8={{180}^{\circ }}\] .
So, we can conclude that the angles \[1=3=5=7\] and \[2=4=6=8\] and \[1+8={{180}^{\circ }}\] .