
In fig, if ${f_1}$, ${f_2}$ and $T$ are the frictional forces on $2{{kg}}$ block, $3{{kg}}$ block and tension in the string, respectively, then find their values. Initially before applying the forces, tension in string was zero.
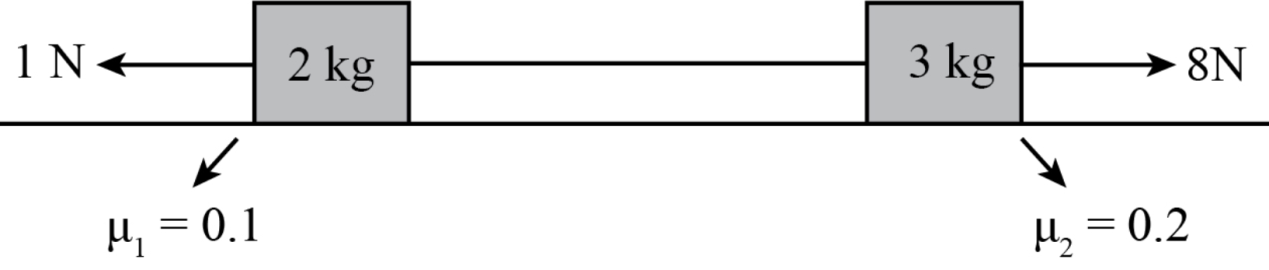

Answer
553.8k+ views
Hint: To solve the problem related to the friction forces, first we have to draw the free body diagram of the given diagram then calculate the all necessary forces required to get the final answer.
Complete step by step answer: Friction is the force which resists the motion of any particle or it is force acting between two surfaces which are in contact with each other and are in motion. The friction force always acts in the opposite direction of the motion.
The formula to calculate the friction force is given as follows.
$f = \mu N$
Here, $\mu $ is friction coefficients, $f$ is friction force, and $N$ is normal force acting on the object.
Draw the free body diagram of the given diagram.
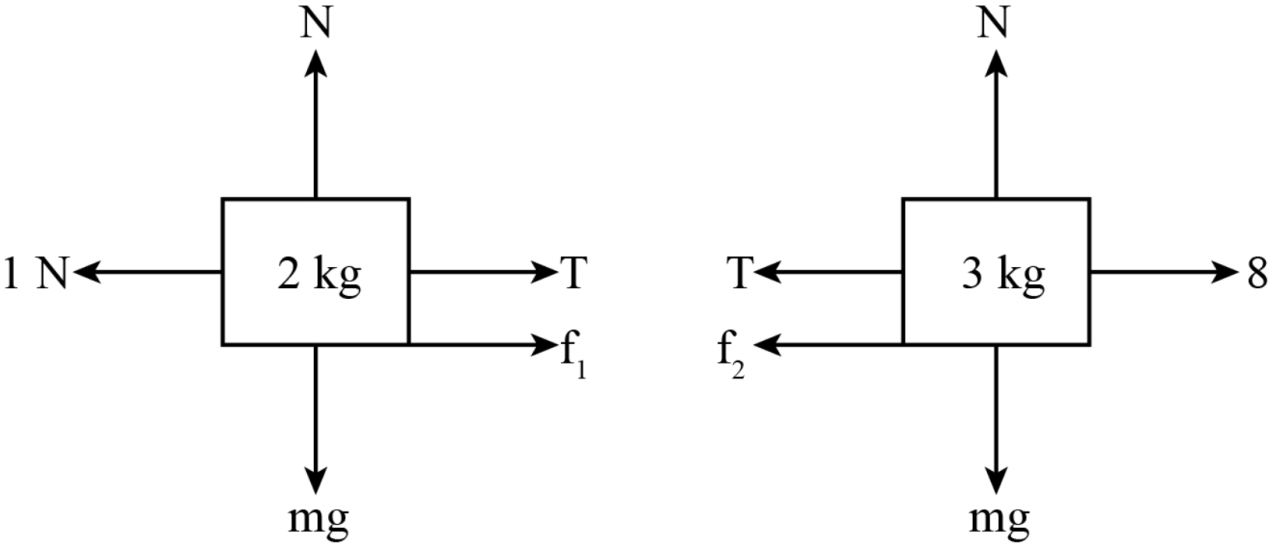
Consider the $3{{kg}}$ block.
Find the normal force $N$ as follows.
$N = mg$
By substituting $3{{kg}}$ for $m$, and $10{{m/}}{{{s}}^{{2}}}$ for $g$ in the equation $N = mg$, we get,
$
N = \left( {3{{kg}}} \right)\left( {10{{m/}}{{{s}}^{{2}}}} \right)\\
= 30{{N}}
$
Find the frictional force in $3{{kg}}$ block.
${f_2} = \mu N$
By substituting $30{{N}}$ for $N$, and $0.2$ for $\mu $, we get,
$
{f_2} = \left( {0.2} \right)\left( {30{{N}}} \right)\\
= 6{{N}}
$
Balance the force on $3{{kg}}$ block to find the tension $\left( T \right)$.
${f_2} + T = 8{{N}}$
By substituting $6{{N}}$ for ${f_2}$ in the equation ${f_2} + T = 8{{N}}$, we get,
$
6{{N}} + T = 8{{N}}\\
\Rightarrow {{T}} = 8{{N}} - 6{{N}}\\
= 2{{N}}
$
Balance the force on $3{{kg}}$ block to find the friction force ${f_2}$.
$T + {f_2} = 1{{N}}$
By substituting $2{{N}}$ for $T$ in the equation $T + {f_2} = 1{{N}}$, we get,
$
2{{N}} + {f_1} = 1{{N}} \\
\Rightarrow {f_1} = 1{{N}} - 2{{N}} \\
= - 1{{N}}
$
The sign is negative so change the direction of ${f_1}$ as shown below.
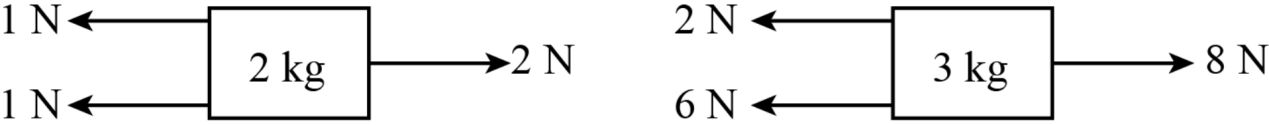
Therefore, the values of ${f_1}$, ${f_2}$ and $T$ are $1{{N}}$, $6{{N}}$, and $2{{N}}$, respectively.
Note: In this problem, the acceleration due to gravity is not given so take $g =
10{{m/}}{{{s}}^{{2}}}$. The key part of this problem is a free body diagram which should be drawn in the correct manner which means the direction of each force will be correct otherwise the solution will be wrong.
Complete step by step answer: Friction is the force which resists the motion of any particle or it is force acting between two surfaces which are in contact with each other and are in motion. The friction force always acts in the opposite direction of the motion.
The formula to calculate the friction force is given as follows.
$f = \mu N$
Here, $\mu $ is friction coefficients, $f$ is friction force, and $N$ is normal force acting on the object.
Draw the free body diagram of the given diagram.

Consider the $3{{kg}}$ block.
Find the normal force $N$ as follows.
$N = mg$
By substituting $3{{kg}}$ for $m$, and $10{{m/}}{{{s}}^{{2}}}$ for $g$ in the equation $N = mg$, we get,
$
N = \left( {3{{kg}}} \right)\left( {10{{m/}}{{{s}}^{{2}}}} \right)\\
= 30{{N}}
$
Find the frictional force in $3{{kg}}$ block.
${f_2} = \mu N$
By substituting $30{{N}}$ for $N$, and $0.2$ for $\mu $, we get,
$
{f_2} = \left( {0.2} \right)\left( {30{{N}}} \right)\\
= 6{{N}}
$
Balance the force on $3{{kg}}$ block to find the tension $\left( T \right)$.
${f_2} + T = 8{{N}}$
By substituting $6{{N}}$ for ${f_2}$ in the equation ${f_2} + T = 8{{N}}$, we get,
$
6{{N}} + T = 8{{N}}\\
\Rightarrow {{T}} = 8{{N}} - 6{{N}}\\
= 2{{N}}
$
Balance the force on $3{{kg}}$ block to find the friction force ${f_2}$.
$T + {f_2} = 1{{N}}$
By substituting $2{{N}}$ for $T$ in the equation $T + {f_2} = 1{{N}}$, we get,
$
2{{N}} + {f_1} = 1{{N}} \\
\Rightarrow {f_1} = 1{{N}} - 2{{N}} \\
= - 1{{N}}
$
The sign is negative so change the direction of ${f_1}$ as shown below.
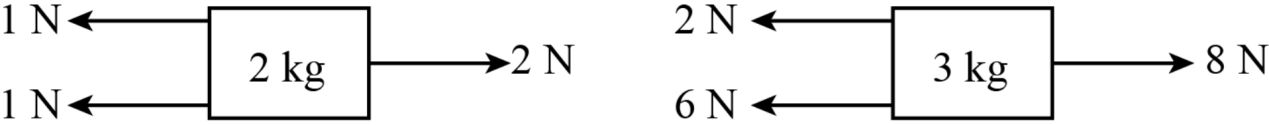
Therefore, the values of ${f_1}$, ${f_2}$ and $T$ are $1{{N}}$, $6{{N}}$, and $2{{N}}$, respectively.
Note: In this problem, the acceleration due to gravity is not given so take $g =
10{{m/}}{{{s}}^{{2}}}$. The key part of this problem is a free body diagram which should be drawn in the correct manner which means the direction of each force will be correct otherwise the solution will be wrong.
Recently Updated Pages
Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Master Class 11 Chemistry: Engaging Questions & Answers for Success

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE

10 examples of friction in our daily life

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE




