Question

In fig, ABCD is a quadrilateral. BE∥AC.BE meets DC (produced) at E.AE and BC intersects at O. Which one is the correct answer from the following?

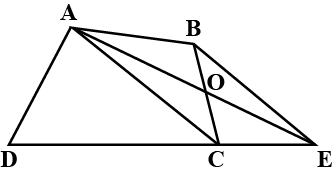
A) ABEC is a parallelogram
B)\[ar\left( \Delta AOC \right)=ar(\Delta BOE)\]
C) \[ar\left( \Delta OAB \right)=ar(\Delta OCE)\]
D) \[ar\left( \Delta ABE \right)=ar(\Delta ACE)\]

Answer 1

Hint: To solve this question the basic fundamental properties of a parallelogram should be well known.
Which are, consider a parallelogram ABCD as shown below

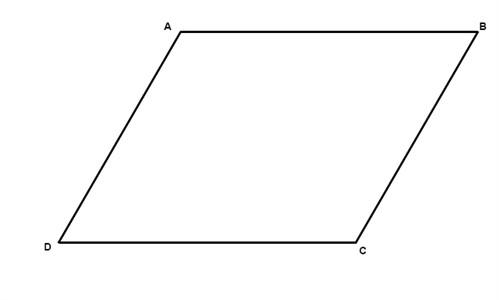
1. Opposite sides are congruent (AB=DC)
2. Opposite angles are congruent ( D=B)
3. Consecutive angles are supplementary (A+D= 180°)
4.The diagonals of a parallelogram bisect each other
5. Each diagonal of a parallelogram separates it into two congruent triangles
6.If one angle is right, then all angles are right.

Complete step by step answer:
Now from the question we can say that, BE||AC
First, let us consider the two triangles \[\Delta AOC\] and\[\Delta BOE\],
As AE and BC intersect at O , we will have alternate angles ( the angles that are in opposite positions relative to a transversal intersecting two lines)
So from the above statement we can say that
\[\angle EBC=\angle BCA,\angle CAE=\angle BEA\] as they are alternate angles
Hence here in \[\Delta AOC\] and\[\Delta BOE\], two of the three angles of a triangle are common so as the sum of all interior angles of a triangle is 180° the third angle of both the triangles would also be the same.
\[\angle AOC=\angle BOE\]
We can here conclude that the triangles \[\Delta AOC\] and\[\Delta BOE\]are similar by AAA(angle-angle-angle) theorem.
Now here BC is a straight line which is intersected by AE at O,
\[\begin{align}
  & \angle AOB+\angle AOC={{180}^{\circ }} \\
 &\Rightarrow \angle AOB=~{{180}^{\circ }}-\angle AOC \\
\end{align}\]
Similarly, AE is a straight line which is intersected by CB at O,
\[\begin{align}
  & \angle COA+\angle COE={{180}^{\circ }} \\
 & \Rightarrow \angle COE=~{{180}^{\circ }}-\angle AOC \\
\end{align}\]
Therefore, \[\angle AOB=\angle COE\]
Now consider \[\Delta AOB\] and\[\Delta EOC\]
The side AO is proportional to OE
The side CO is proportional to OB
And also \[\angle AOB=\angle COE\]
From the above three statements we can conclude that \[\Delta AOB\] and\[\Delta EOC\] are similar by SAS(side-angle-side) theorem.
So,
\[\angle ABC=\angle BCE\] and \[\angle BAE=\angle AEC\] by the property of similar triangles.
Therefore we can conclude from the above statements that AB||CE, BE||AC the opposite sides are congruent, opposite angles are congruent and the consecutive angles are supplementary.

So, the correct answer is “Option A”.

Note: Students should be well aware of the properties of parallel lines, intersecting lines and the theorems of similarity like SAS,SSS,AAA which will be quite useful while solving problems related to similar triangles. The angles should be named and measured accurately for no further queries.