
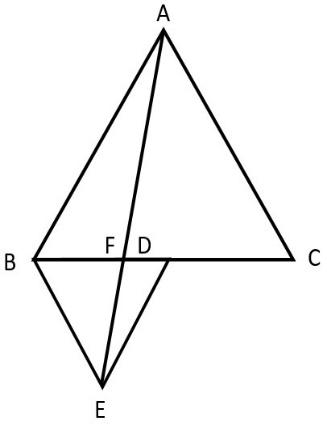
In fig, ABC and BDE are two equilateral triangles such that D is the midpoint of BC. If AE intersects BC at F, show that
(i) ar(ADE) =$\dfrac{1}{4}$ ar(ABC)
(ii) ar(BDE) = $\dfrac{1}{2}$ ar(BAE)
(iii) ar(ABC) = 2 ar(BEC)
(iv) ar(BFE) = ar(AFD)
(v) ar(BFE) = 2 ar(FED)
(vi) ar(FED) = $\dfrac{1}{8}$ ar(AFC)

Answer
597.9k+ views
Hint: Here in the figure join AD, EC, draw EL $\bot $BD. For the equilateral triangle $\Delta ABC$, since D is the midpoint, AD is the median as well as altitude. Similarly EL is the median and altitude of the equilateral triangle $\Delta BDE$. Here, we have to consider the theorem that the triangle on the same base and between the same parallels are equal in area and also use the property that the median divides the triangle into two triangles of equal area.
Complete step by step answer:
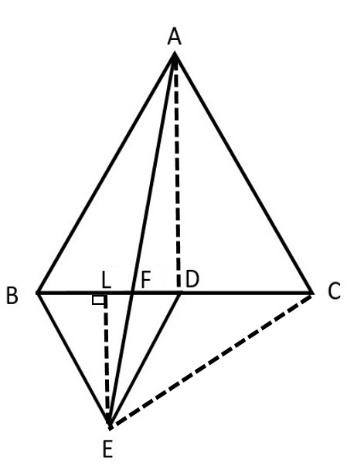
Here, given that ABC and BDE are two equilateral triangles such that D is the midpoint of BC, AE intersects BC at F.
Now, we have to prove that:
ar(ADE) =$\dfrac{1}{4}$ ar(ABC)
First join AD and EC, draw EL $\bot $ BD.
Given that $\Delta ABC$ is an equilateral triangle. We know that in an equilateral triangle all sides are equal and each angle is ${{60}^{\circ }}$.
Here, let AB = AC = BC = 2a and
\[~\angle ABC\text{ }=~\angle ACB\text{ }=\angle ~BAC\text{ }={{60}^{\circ }}\]. Since D is the midpoint of BC, we can say that BD = DC, i.e.
BC = BD + DC
BC = 2BD
Since, BC = 2a we can write:
2a = 2BD
By cross multiplication we get:
BD = $\dfrac{2a}{a}$
Hence, by cancellation we get:
BD = a
Hence, we got BD = DC = a
Now, consider the equilateral triangle $\Delta BDE$. Here, we will get:
BD = BE = ED = a,
$\angle BED=~\angle BDE=~\angle EBD={{60}^{{}^\circ }}$
Next, since D is the midpoint of BC we can say that AD is the median. We also know by a theorem that the median of an equilateral triangle is perpendicular to the third side.
Therefore, we can say that AD is the altitude. i.e.
$AD\bot BC$
Hence, $\Delta ADC$ and $\Delta ADB$ are right angled triangles.
Consider, $\Delta ADC$
By Pythagoras theorem we can say that,
$A{{C}^{2}}=A{{D}^{2}}+D{{C}^{2}}$
We know that AC = 2a and DC = a. Therefore, we will get:
$\begin{align}
& {{(2a)}^{2}}=A{{D}^{2}}+{{a}^{2}}^{{}} \\
& 4{{a}^{2}}=A{{D}^{2}}+{{a}^{2}}^{{}} \\
& A{{D}^{2}}=4{{a}^{2}}-{{a}^{2}}^{{}} \\
& A{{D}^{2}}=3{{a}^{2}} \\
\end{align}$
By taking square root on both the sides we get:
$\begin{align}
& \sqrt{A{{D}^{2}}}=\sqrt{3{{a}^{2}}} \\
& AD=\pm \sqrt{3}a \\
\end{align}$
Since, the side is a positive value we can say that:
$AD=\sqrt{3}a$
Similarly consider the equilateral triangle $\Delta BDE$.
Since, $EL\bot BD$, we can say a perpendicular line drawn to the opposite side of an equilateral triangle bisects the opposite side. Therefore L is the midpoint of BD, BL = LD, i.e. EL is the median.
Hence, we can write:
BD = BL + LD
BD= BL + BL
BD = 2BL
Since BD = a, we have:
a = 2BL
BL = $\dfrac{a}{2}$
Now, let us consider the right triangle$\Delta BLE$. Hence by Pythagoras theorem, we have:
$B{{E}^{2}}=B{{L}^{2}}+E{{L}^{2}}$
We know that $BE=a$ and $BL=\dfrac{a}{2}$. Hence we will get:
$\begin{align}
& {{a}^{2}}={{\left( \dfrac{a}{2} \right)}^{2}}+E{{L}^{2}} \\
& {{a}^{2}}=\dfrac{{{a}^{2}}}{4}+E{{L}^{2}} \\
& {{a}^{2}}-\dfrac{{{a}^{2}}}{4}=E{{L}^{2}} \\
\end{align}$
By taking the LCM we will get:
$\begin{align}
& \dfrac{4{{a}^{2}}-{{a}^{2}}}{4}=E{{L}^{2}} \\
& \dfrac{3{{a}^{2}}}{4}=E{{L}^{2}} \\
\end{align}$
Hence, by taking square root on both the sides we obtain:
$\begin{align}
& \sqrt{EL}=\sqrt{\dfrac{3}{4}{{a}^{2}}} \\
& EL=\dfrac{\sqrt{3}}{2}a \\
\end{align}$
Next, we have to find the areas of $\Delta ABC$ and $\Delta ADE$.
First consider $\Delta ABC$
We know that the area of the triangle when base and height are given is:
Area = $\dfrac{1}{2}$ Base $\times $ Height
Here Base, BC = 2a
Height, AD = $\sqrt{3}a$
.Hence we will obtain:
\[\begin{align}
& ar\left( ABC \right)\text{ }=\dfrac{1}{2}\times BC\times AD \\
& ar\left( ABC \right)\text{ }=\dfrac{1}{2}\times 2a\times \sqrt{3}a \\
& ar\left( ABC \right)\text{ }=\sqrt{3}{{a}^{2}} \\
\end{align}\]
Now, consider $\Delta ADE$ we have:
Base, ED = a
Height, EL = $\dfrac{\sqrt{3}}{2}a$
Hence, the area of ADE = $\dfrac{1}{2}$ Base $\times $ Height
\[\begin{align}
& ar\left( ADE \right)\text{ }=\dfrac{1}{2}\times ED\times EL \\
& ar\left( ADE \right)\text{ }=\dfrac{1}{2}\times a\times \dfrac{\sqrt{3}}{2}a \\
& ar\left( ADE \right)\text{ }=\dfrac{\sqrt{3}}{4}{{a}^{2}} \\
\end{align}\]
Now, by dividing the area we obtain:
$\begin{align}
& \dfrac{ar(ADE)}{ar(ABC)}=\dfrac{\dfrac{\sqrt{3}}{4}{{a}^{2}}}{\sqrt{3}{{a}^{2}}} \\
& \dfrac{ar(ADE)}{ar(ABC)}=\dfrac{\sqrt{3}{{a}^{2}}}{4\times \sqrt{3}{{a}^{2}}} \\
\end{align}$
By cancellation we get:
$\dfrac{ar(ADE)}{ar(ABC)}=\dfrac{1}{4}$
By cross multiplication, we obtain:
$ar(ADE)=\dfrac{1}{4}ar(ABC)$
Hence, the proof.
ar(BDE) = $\dfrac{1}{2}$ ar(BAE)
We can say that for equilateral triangles $\Delta ABC$ and $\Delta BDE$ we have:
$\angle ACB=\angle EBC={{60}^{\circ }}$
For lines BE and AC, consider the transversal BC. Then, they are alternate interior angles. We know that if alternate interior angles are equal then the corresponding lines are parallel.
$BE\parallel AC$
Consider triangles $\Delta BAE$ and $\Delta BCE$.We can say that the triangles are on the same base BE and between the same parallels BE and AC
We know that the triangles on the same base and between the same parallels are equal.
Therefore we can write:
$ar(BAE)=ar(BCE)$ …. (1)
Now, consider $\Delta BCE$, we can write:
$ar(BCE)=ar(BDE)+ar(CDE)$
D is the midpoint of BC, so ED is the median.
We have a theorem that median divides a triangle into two triangles of equal area.
Therefore, we can say that,
$ar(BDE)=ar(CDE)$.
Hence, we will get:
$\begin{align}
& ar(BCE)=ar(BDE)+ar(BDE) \\
& ar(BCE)=2ar(BDE)\text{ }.....\text{ (2)} \\
\end{align}$
By substituting the equation (2) in equation (1) we obtain:
$ar(BAE)=2ar(BDE)$
By cross multiplication we get:
$ar(BDE)=\dfrac{1}{2}ar(BAE)$
Hence the proof.
To prove $ar(ABC)=2ar(BEC)$
Here, in the first part we have already proved that:
$ar(BDE)=\dfrac{1}{4}ar(ABC)$ …. (3)
We also proved that:
$ar(BCE)=2ar(BDE)$
Hence by cross multiplication we can say that:
$ar(BDE)=\dfrac{1}{2}ar(BCE)$ ….. (4)
Therefore by equation (3) and equation (4) we will obtain:
$\begin{align}
& \dfrac{1}{4}ar(ABC)=\dfrac{1}{2}ar(BCE) \\
& \Rightarrow \dfrac{1}{2}ar(ABC)=ar(BCE) \\
& \Rightarrow ar(ABC)=2ar(BCE) \\
\end{align}$
Hence, we can say that, $ar(ABC)=2ar(BEC)$
To prove that $ar(BFE)=ar(AFD)$.
For that consider the equilateral triangles $\Delta ABC$ and $\Delta BDE$.
$\angle ABC=\angle BDE={{60}^{\circ }}$, which are alternate interior angles.
For the lines AB and ED, consider the transversal BD. We know that if the alternate interior angles are equal, then the corresponding lines are parallel. Hence we can say that:
$AB\parallel ED$
We know that the triangles on the same base and between the same parallels are equal in area. Therefore we get:
$ar(BED)=ar(AED)$
Now, by subtracting $ar(FED)$ on both the sides we get:
$\begin{align}
& ar(BED)-ar(FED)=ar(AED)-ar(FED) \\
& ar(BFE)=ar(AFD) \\
\end{align}$
Hence the proof.
To prove that $ar(BFE)=2ar(FED)$.
Here, consider the triangles $\Delta BFE$ and $\Delta FED$.
In $\Delta BFE$, Base = BF, Height = EL
In $\Delta FED$, Base = FD, Height = EL
We have $EL=\dfrac{\sqrt{3}}{2}a$
Now, consider the areas of $\Delta BFE$ and $\Delta FED$
Area of a triangle = $\dfrac{1}{2}$ Base $\times$ Height
$ar(BFE)=\dfrac{1}{2}\times BF\times EL$ ….. (5)
$ar(FED)=\dfrac{1}{2}\times FD\times EL$ …… (6)
Now by dividing equation (5) by equation (6) we get:
$\dfrac{ar(BFE)}{ar(AFD)}=\dfrac{\dfrac{1}{2}\times BF\times EL}{\dfrac{1}{2}\times FD\times EL}$
Now, by cancellation we obtain:
$\dfrac{ar(BFE)}{ar(AFD)}=\dfrac{BF}{FD}$
Now, we have to find BF and FD.
We have already proved that:
$ar(AFD)=ar(BFE)$ …. (7)
Now find the areas of $\Delta AFD$ and $\Delta BFE$
$ar(AFD)=\dfrac{1}{2}\times FD\times AD$
We have $AD=\sqrt{3}a$. Therefore, we will get:
$ar(AFD)=\dfrac{1}{2}\times FD\times \sqrt{3}a$ ….. (8)
Now,
$ar(BFE)=\dfrac{1}{2}\times BF\times EL$
We have $EL=\dfrac{\sqrt{3}}{2}a$
$ar(BFE)=\dfrac{1}{2}\times BF\times \dfrac{\sqrt{3}}{2}a$ …. (9)
By substituting equation (8) and equation (9) in equation (7) we get:
$\dfrac{1}{2}\times FD\times \sqrt{3}a=\dfrac{1}{2}\times BF\times \dfrac{\sqrt{3}}{2}a$
By cross multiplication we get:
$FD=\dfrac{BF}{2}$
By cross multiplication we obtain:
$BF=2FD$
We have:
$\begin{align}
& \dfrac{ar(BFE)}{ar(AFD)}=\dfrac{BF}{FD} \\
& \dfrac{ar(BFE)}{ar(AFD)}=\dfrac{2FD}{FD} \\
\end{align}$
Now by cancellation we obtain:
$\begin{align}
& \dfrac{ar(BFE)}{ar(AFD)}=2 \\
& ar(BFE)=2ar(AFD) \\
\end{align}$
Hence the proof.
To prove $ar(FED)=\dfrac{1}{8}ar(AFC)$
Here, consider the $\Delta FED$ . We have to find the area.
Given that the base is FD, height is EL
First let us calculate FD.
We have:
BD = BF + FD
We have proved that:
BF = 2 FD
Hence we will get:
BD = 2FD + FD
BD = 3FD
We know that BD = a. Therefore we will obtain:
a = 3FD
By cross multiplication we get:
FD = $\dfrac{a}{3}$
Now consider the area:
$\begin{align}
& ar(FED)=\dfrac{1}{2}\times FD\times EL \\
& ar(FED)=\dfrac{1}{2}\times \dfrac{a}{3}\times \dfrac{\sqrt{3}}{2}a \\
& ar(FED)=\dfrac{\sqrt{3}}{12}{{a}^{2}} \\
\end{align}$
Now, consider $\Delta AFC$, we have to find an area.
We have the base FC and height AD.
We can write:
$\begin{align}
& FC=FD+DC \\
& FC=\dfrac{a}{3}+a \\
& FC=\dfrac{a+3a}{3} \\
& FC=\dfrac{4}{3}a \\
\end{align}$
Aw know that $AD=\sqrt{3}a$
Therefore, the area can be written as:
$\begin{align}
& ar(AFC)=\dfrac{1}{2}\times FC\times AD \\
& ar(AFC)=\dfrac{1}{2}\times \dfrac{4}{3}a\times \sqrt{3}a \\
& ar(AFC)=\dfrac{2\sqrt{3}}{3}{{a}^{2}} \\
\end{align}$
Now, by dividing we get:
$\begin{align}
& \dfrac{ar(FED)}{ar(AFC)}=\dfrac{\dfrac{\sqrt{3}}{12}{{a}^{2}}}{\dfrac{2\sqrt{3}}{3}{{a}^{2}}} \\
& \dfrac{ar(FED)}{ar(AFC)}=\dfrac{\sqrt{3}}{12}{{a}^{2}}\times \dfrac{3}{2\sqrt{3}{{a}^{2}}} \\
\end{align}$
Now, by cancellation we obtain:
$\begin{align}
& \dfrac{ar(FED)}{ar(AFC)}=\dfrac{1}{8} \\
& ar(FED)=\dfrac{1}{8}ar(AFC) \\
\end{align}$
Hence the proof.
Note: Here, $EL\bot BD$, therefore El is the height of $\Delta BDE,\Delta BFE$ and $\Delta EFD$. While equating the areas you should be careful, check whether it has the same base and lying between the same parallels.
Complete step by step answer:

Here, given that ABC and BDE are two equilateral triangles such that D is the midpoint of BC, AE intersects BC at F.
Now, we have to prove that:
ar(ADE) =$\dfrac{1}{4}$ ar(ABC)
First join AD and EC, draw EL $\bot $ BD.
Given that $\Delta ABC$ is an equilateral triangle. We know that in an equilateral triangle all sides are equal and each angle is ${{60}^{\circ }}$.
Here, let AB = AC = BC = 2a and
\[~\angle ABC\text{ }=~\angle ACB\text{ }=\angle ~BAC\text{ }={{60}^{\circ }}\]. Since D is the midpoint of BC, we can say that BD = DC, i.e.
BC = BD + DC
BC = 2BD
Since, BC = 2a we can write:
2a = 2BD
By cross multiplication we get:
BD = $\dfrac{2a}{a}$
Hence, by cancellation we get:
BD = a
Hence, we got BD = DC = a
Now, consider the equilateral triangle $\Delta BDE$. Here, we will get:
BD = BE = ED = a,
$\angle BED=~\angle BDE=~\angle EBD={{60}^{{}^\circ }}$
Next, since D is the midpoint of BC we can say that AD is the median. We also know by a theorem that the median of an equilateral triangle is perpendicular to the third side.
Therefore, we can say that AD is the altitude. i.e.
$AD\bot BC$
Hence, $\Delta ADC$ and $\Delta ADB$ are right angled triangles.
Consider, $\Delta ADC$
By Pythagoras theorem we can say that,
$A{{C}^{2}}=A{{D}^{2}}+D{{C}^{2}}$
We know that AC = 2a and DC = a. Therefore, we will get:
$\begin{align}
& {{(2a)}^{2}}=A{{D}^{2}}+{{a}^{2}}^{{}} \\
& 4{{a}^{2}}=A{{D}^{2}}+{{a}^{2}}^{{}} \\
& A{{D}^{2}}=4{{a}^{2}}-{{a}^{2}}^{{}} \\
& A{{D}^{2}}=3{{a}^{2}} \\
\end{align}$
By taking square root on both the sides we get:
$\begin{align}
& \sqrt{A{{D}^{2}}}=\sqrt{3{{a}^{2}}} \\
& AD=\pm \sqrt{3}a \\
\end{align}$
Since, the side is a positive value we can say that:
$AD=\sqrt{3}a$
Similarly consider the equilateral triangle $\Delta BDE$.
Since, $EL\bot BD$, we can say a perpendicular line drawn to the opposite side of an equilateral triangle bisects the opposite side. Therefore L is the midpoint of BD, BL = LD, i.e. EL is the median.
Hence, we can write:
BD = BL + LD
BD= BL + BL
BD = 2BL
Since BD = a, we have:
a = 2BL
BL = $\dfrac{a}{2}$
Now, let us consider the right triangle$\Delta BLE$. Hence by Pythagoras theorem, we have:
$B{{E}^{2}}=B{{L}^{2}}+E{{L}^{2}}$
We know that $BE=a$ and $BL=\dfrac{a}{2}$. Hence we will get:
$\begin{align}
& {{a}^{2}}={{\left( \dfrac{a}{2} \right)}^{2}}+E{{L}^{2}} \\
& {{a}^{2}}=\dfrac{{{a}^{2}}}{4}+E{{L}^{2}} \\
& {{a}^{2}}-\dfrac{{{a}^{2}}}{4}=E{{L}^{2}} \\
\end{align}$
By taking the LCM we will get:
$\begin{align}
& \dfrac{4{{a}^{2}}-{{a}^{2}}}{4}=E{{L}^{2}} \\
& \dfrac{3{{a}^{2}}}{4}=E{{L}^{2}} \\
\end{align}$
Hence, by taking square root on both the sides we obtain:
$\begin{align}
& \sqrt{EL}=\sqrt{\dfrac{3}{4}{{a}^{2}}} \\
& EL=\dfrac{\sqrt{3}}{2}a \\
\end{align}$
Next, we have to find the areas of $\Delta ABC$ and $\Delta ADE$.
First consider $\Delta ABC$
We know that the area of the triangle when base and height are given is:
Area = $\dfrac{1}{2}$ Base $\times $ Height
Here Base, BC = 2a
Height, AD = $\sqrt{3}a$
.Hence we will obtain:
\[\begin{align}
& ar\left( ABC \right)\text{ }=\dfrac{1}{2}\times BC\times AD \\
& ar\left( ABC \right)\text{ }=\dfrac{1}{2}\times 2a\times \sqrt{3}a \\
& ar\left( ABC \right)\text{ }=\sqrt{3}{{a}^{2}} \\
\end{align}\]
Now, consider $\Delta ADE$ we have:
Base, ED = a
Height, EL = $\dfrac{\sqrt{3}}{2}a$
Hence, the area of ADE = $\dfrac{1}{2}$ Base $\times $ Height
\[\begin{align}
& ar\left( ADE \right)\text{ }=\dfrac{1}{2}\times ED\times EL \\
& ar\left( ADE \right)\text{ }=\dfrac{1}{2}\times a\times \dfrac{\sqrt{3}}{2}a \\
& ar\left( ADE \right)\text{ }=\dfrac{\sqrt{3}}{4}{{a}^{2}} \\
\end{align}\]
Now, by dividing the area we obtain:
$\begin{align}
& \dfrac{ar(ADE)}{ar(ABC)}=\dfrac{\dfrac{\sqrt{3}}{4}{{a}^{2}}}{\sqrt{3}{{a}^{2}}} \\
& \dfrac{ar(ADE)}{ar(ABC)}=\dfrac{\sqrt{3}{{a}^{2}}}{4\times \sqrt{3}{{a}^{2}}} \\
\end{align}$
By cancellation we get:
$\dfrac{ar(ADE)}{ar(ABC)}=\dfrac{1}{4}$
By cross multiplication, we obtain:
$ar(ADE)=\dfrac{1}{4}ar(ABC)$
Hence, the proof.
ar(BDE) = $\dfrac{1}{2}$ ar(BAE)
We can say that for equilateral triangles $\Delta ABC$ and $\Delta BDE$ we have:
$\angle ACB=\angle EBC={{60}^{\circ }}$
For lines BE and AC, consider the transversal BC. Then, they are alternate interior angles. We know that if alternate interior angles are equal then the corresponding lines are parallel.
$BE\parallel AC$
Consider triangles $\Delta BAE$ and $\Delta BCE$.We can say that the triangles are on the same base BE and between the same parallels BE and AC
We know that the triangles on the same base and between the same parallels are equal.
Therefore we can write:
$ar(BAE)=ar(BCE)$ …. (1)
Now, consider $\Delta BCE$, we can write:
$ar(BCE)=ar(BDE)+ar(CDE)$
D is the midpoint of BC, so ED is the median.
We have a theorem that median divides a triangle into two triangles of equal area.
Therefore, we can say that,
$ar(BDE)=ar(CDE)$.
Hence, we will get:
$\begin{align}
& ar(BCE)=ar(BDE)+ar(BDE) \\
& ar(BCE)=2ar(BDE)\text{ }.....\text{ (2)} \\
\end{align}$
By substituting the equation (2) in equation (1) we obtain:
$ar(BAE)=2ar(BDE)$
By cross multiplication we get:
$ar(BDE)=\dfrac{1}{2}ar(BAE)$
Hence the proof.
To prove $ar(ABC)=2ar(BEC)$
Here, in the first part we have already proved that:
$ar(BDE)=\dfrac{1}{4}ar(ABC)$ …. (3)
We also proved that:
$ar(BCE)=2ar(BDE)$
Hence by cross multiplication we can say that:
$ar(BDE)=\dfrac{1}{2}ar(BCE)$ ….. (4)
Therefore by equation (3) and equation (4) we will obtain:
$\begin{align}
& \dfrac{1}{4}ar(ABC)=\dfrac{1}{2}ar(BCE) \\
& \Rightarrow \dfrac{1}{2}ar(ABC)=ar(BCE) \\
& \Rightarrow ar(ABC)=2ar(BCE) \\
\end{align}$
Hence, we can say that, $ar(ABC)=2ar(BEC)$
To prove that $ar(BFE)=ar(AFD)$.
For that consider the equilateral triangles $\Delta ABC$ and $\Delta BDE$.
$\angle ABC=\angle BDE={{60}^{\circ }}$, which are alternate interior angles.
For the lines AB and ED, consider the transversal BD. We know that if the alternate interior angles are equal, then the corresponding lines are parallel. Hence we can say that:
$AB\parallel ED$
We know that the triangles on the same base and between the same parallels are equal in area. Therefore we get:
$ar(BED)=ar(AED)$
Now, by subtracting $ar(FED)$ on both the sides we get:
$\begin{align}
& ar(BED)-ar(FED)=ar(AED)-ar(FED) \\
& ar(BFE)=ar(AFD) \\
\end{align}$
Hence the proof.
To prove that $ar(BFE)=2ar(FED)$.
Here, consider the triangles $\Delta BFE$ and $\Delta FED$.
In $\Delta BFE$, Base = BF, Height = EL
In $\Delta FED$, Base = FD, Height = EL
We have $EL=\dfrac{\sqrt{3}}{2}a$
Now, consider the areas of $\Delta BFE$ and $\Delta FED$
Area of a triangle = $\dfrac{1}{2}$ Base $\times$ Height
$ar(BFE)=\dfrac{1}{2}\times BF\times EL$ ….. (5)
$ar(FED)=\dfrac{1}{2}\times FD\times EL$ …… (6)
Now by dividing equation (5) by equation (6) we get:
$\dfrac{ar(BFE)}{ar(AFD)}=\dfrac{\dfrac{1}{2}\times BF\times EL}{\dfrac{1}{2}\times FD\times EL}$
Now, by cancellation we obtain:
$\dfrac{ar(BFE)}{ar(AFD)}=\dfrac{BF}{FD}$
Now, we have to find BF and FD.
We have already proved that:
$ar(AFD)=ar(BFE)$ …. (7)
Now find the areas of $\Delta AFD$ and $\Delta BFE$
$ar(AFD)=\dfrac{1}{2}\times FD\times AD$
We have $AD=\sqrt{3}a$. Therefore, we will get:
$ar(AFD)=\dfrac{1}{2}\times FD\times \sqrt{3}a$ ….. (8)
Now,
$ar(BFE)=\dfrac{1}{2}\times BF\times EL$
We have $EL=\dfrac{\sqrt{3}}{2}a$
$ar(BFE)=\dfrac{1}{2}\times BF\times \dfrac{\sqrt{3}}{2}a$ …. (9)
By substituting equation (8) and equation (9) in equation (7) we get:
$\dfrac{1}{2}\times FD\times \sqrt{3}a=\dfrac{1}{2}\times BF\times \dfrac{\sqrt{3}}{2}a$
By cross multiplication we get:
$FD=\dfrac{BF}{2}$
By cross multiplication we obtain:
$BF=2FD$
We have:
$\begin{align}
& \dfrac{ar(BFE)}{ar(AFD)}=\dfrac{BF}{FD} \\
& \dfrac{ar(BFE)}{ar(AFD)}=\dfrac{2FD}{FD} \\
\end{align}$
Now by cancellation we obtain:
$\begin{align}
& \dfrac{ar(BFE)}{ar(AFD)}=2 \\
& ar(BFE)=2ar(AFD) \\
\end{align}$
Hence the proof.
To prove $ar(FED)=\dfrac{1}{8}ar(AFC)$
Here, consider the $\Delta FED$ . We have to find the area.
Given that the base is FD, height is EL
First let us calculate FD.
We have:
BD = BF + FD
We have proved that:
BF = 2 FD
Hence we will get:
BD = 2FD + FD
BD = 3FD
We know that BD = a. Therefore we will obtain:
a = 3FD
By cross multiplication we get:
FD = $\dfrac{a}{3}$
Now consider the area:
$\begin{align}
& ar(FED)=\dfrac{1}{2}\times FD\times EL \\
& ar(FED)=\dfrac{1}{2}\times \dfrac{a}{3}\times \dfrac{\sqrt{3}}{2}a \\
& ar(FED)=\dfrac{\sqrt{3}}{12}{{a}^{2}} \\
\end{align}$
Now, consider $\Delta AFC$, we have to find an area.
We have the base FC and height AD.
We can write:
$\begin{align}
& FC=FD+DC \\
& FC=\dfrac{a}{3}+a \\
& FC=\dfrac{a+3a}{3} \\
& FC=\dfrac{4}{3}a \\
\end{align}$
Aw know that $AD=\sqrt{3}a$
Therefore, the area can be written as:
$\begin{align}
& ar(AFC)=\dfrac{1}{2}\times FC\times AD \\
& ar(AFC)=\dfrac{1}{2}\times \dfrac{4}{3}a\times \sqrt{3}a \\
& ar(AFC)=\dfrac{2\sqrt{3}}{3}{{a}^{2}} \\
\end{align}$
Now, by dividing we get:
$\begin{align}
& \dfrac{ar(FED)}{ar(AFC)}=\dfrac{\dfrac{\sqrt{3}}{12}{{a}^{2}}}{\dfrac{2\sqrt{3}}{3}{{a}^{2}}} \\
& \dfrac{ar(FED)}{ar(AFC)}=\dfrac{\sqrt{3}}{12}{{a}^{2}}\times \dfrac{3}{2\sqrt{3}{{a}^{2}}} \\
\end{align}$
Now, by cancellation we obtain:
$\begin{align}
& \dfrac{ar(FED)}{ar(AFC)}=\dfrac{1}{8} \\
& ar(FED)=\dfrac{1}{8}ar(AFC) \\
\end{align}$
Hence the proof.
Note: Here, $EL\bot BD$, therefore El is the height of $\Delta BDE,\Delta BFE$ and $\Delta EFD$. While equating the areas you should be careful, check whether it has the same base and lying between the same parallels.
Recently Updated Pages
In cricket, what is a "pink ball" primarily used for?

In cricket, what is the "new ball" phase?

In cricket, what is a "death over"?

What is the "Powerplay" in T20 cricket?

In cricket, what is a "super over"?

In cricket, what is a "tail-ender"?

Trending doubts
Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

Write an application to the principal requesting five class 10 english CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Who Won 36 Oscar Awards? Record Holder Revealed




