Question

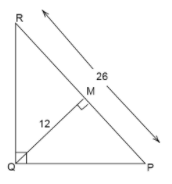
In $\Delta PQR,m\angle Q = {90^0}$ and $\overline {QM} $ is an altitude; $M$ $ \in \overline {PR} $. IF $QM = 12,PR = 26;$ then find $PM$ and RM; If$PM < RM;$ then find $PQ$ and $QR$.

Answer 1

Hint: Here the question shows that triangle is the right-angle triangle as angle Q is 90 degree. First, we have to make a diagram to clarify the question it will help us to understand the question.
               

Complete step-by-step answer:
As given in the question, In a triangle $PQR,m\angle Q$ is ${90^0}$ and $\overline {QM} $ is altitude; $M \in \overline {QM} $
Triangle PQM is correspondence to triangle RMQ hence
Therefore, we have
$P - M - R,Q{M^2} = PM.MR$
We are assuming length of the $PM$ = a
Then $RM = PR - PM$
Value of $PR$ is given in the question
So, $RM = 26 - a$
Now, $Q{M^2} = PM.RM$
$PM$ multiply by $RM$
Then we put the values in equation
${12^2} = a(26 - a)$
Open the brackets
$144 = 26a - {a^2}$
We get $144$ by multiply 12 by 12 (144 is square root of 12)
${a^2} - 26a + 144 = 0$
Use the factorization method to solve the equation
${a^2} - 18a - 8a + 144 = 0$
$a(a - 18) - 8(a - 18) = 0$
$(a - 8)(a - 18) = 0$
$a = 8$ or $a = 18$
So $PM = 8$ and $RM = 18$or $PM = 18$ and $RM = 8$
If $PM < RM$, then $PM = 8$ and $RM = 18$
Now, we will find the value of $PQ$
$P{Q^2} = PM.PR$
Put the values of the equation
$P{Q^2} = 8 \times 26$
$P{Q^2} = 208$
Take the root both side we get
$PQ = 4\sqrt {13} $
Now we find $QR$
$Q{R^2} = RM.PR$
$Q{R^2} = 18 \times 26$
Here we multiply 18 by 26
$Q{R^2} = 468$
$QR = 6\sqrt {13} $

Note: Use the factorization and Pythagoras theorem formula to solve this kind of question and it is good to learn some basic roots. It can help to solve the question fast. Students can use the highest common factor to find the roots, it is the easiest way to solve the roots. You have to read the question carefully what is given and put the values correctly. Like here this is given that RM is greater than PM but students don't notice the signs.