
In $\Delta ABC,XY$||$BC$ and XY divides the triangle into two parts of equal areas. Find $\left( \dfrac{BX}{AB} \right)$.
Answer
624.9k+ views
Hint: We will use the theorem of two similar triangles, which states that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. We will also use the concept of corresponding angles. $A$||$B$ then, $\angle 1=\angle 2$.
Complete step-by-step answer:
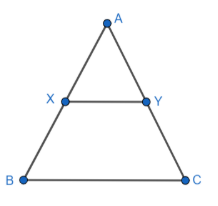
It is given in the question that $ABC$ is a triangle in which $XY$||$BC$ and it divides the area of $\Delta ABC$ into two equal parts. Then, we have to find the value of $\left( \dfrac{BX}{AB} \right)$.
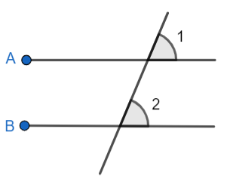
Here, in $\Delta ABC$ side $BC$ is parallel to $XY$. We know that, when two lines are parallel to each other and if a third line passes through both the lines then it is called a transverse line. And the angles made by the parallel and transverse lines are known to be transverse angles.
Since, $\angle 1=\angle 2$ as they are transverse angles. Now, in $\Delta ABC$, we have side$XY$||side$BC$. And side $AB$ and $AC$ are transverse lines for $XY$ and $BC$. So, when $XY$||$BC$ and $AB$ is a transversal line. Then, we get
$\angle AXY=\angle ABC$ ……….(i)
Both are corresponding angles and when $XY$||$BC$ and $AC$ is a transversal line. Then, we get
$\angle AYX=\angle ACB$ ………..(ii)
Then, $\Delta AXY$~$\Delta ABC$ by $AA$(ANGLE-ANGLE) similarity.
Now, we know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. So, we get
$\dfrac{ar(\Delta AXY)}{ar(\Delta ABC)}={{\left( \dfrac{AX}{AB} \right)}^{2}}$
We know that area of $\Delta AXY$=$\dfrac{1}{2}$ area of $\Delta ABC$. From this, we can write $ar(\Delta AXY)$ as $\dfrac{1}{2}ar(\Delta ABC)$
$\Rightarrow \dfrac{\dfrac{1}{2}ar(\Delta ABC)}{ar(\Delta ABC)}={{\left( \dfrac{AX}{AB} \right)}^{2}}$
Cancelling $ar(\Delta ABC)$ from numerator and denominator in L.H.S, we get
$\Rightarrow \dfrac{1}{2}={{\left( \dfrac{AX}{AB} \right)}^{2}}$
$\Rightarrow \dfrac{1}{\sqrt{2}}=\left( \dfrac{AX}{AB} \right)$ ……….(iii)
Now, we can write $AX$ as $(AB-BX)$ in equation (iii), we get
$\Rightarrow \dfrac{AB-BX}{AB}=\dfrac{1}{\sqrt{2}}$ ……….(iv)
On cross multiplying equation (iv), we get
$\Rightarrow \sqrt{2}(AB-BX)=1\times AB$
$\Rightarrow \sqrt{2}(AB-BX)=AB$
$\Rightarrow \sqrt{2}AB-\sqrt{2}BX=AB$
Transposing $-\sqrt{2}BX$ from L.H.S to R.H.S, we get
$\Rightarrow \sqrt{2}AB=AB+\sqrt{2}BX$
Transposing $AB$ from R.H.S to L.H.S, we get
$\Rightarrow \sqrt{2}AB-AB=\sqrt{2}BX$
Taking $AB$ as common in L.H.S, we get
$\Rightarrow AB(\sqrt{2}-1)=\sqrt{2}BX$
$\Rightarrow \sqrt{2}BX=(\sqrt{2}-1)AB$
On dividing by $\sqrt{2}AB$ on both the sides, we get
$\Rightarrow \dfrac{\sqrt{2}BX}{\sqrt{2}AB}=\dfrac{(\sqrt{2}-1)AB}{\sqrt{2}AB}$
$\Rightarrow \dfrac{BX}{AB}=\dfrac{\sqrt{2}-1}{\sqrt{2}}$
Note: You can solve this question by any method of your choice but, the key is you need to know that both $\Delta ABC$ and $\Delta AXY$ are similar to each other. The only possible mistake that can be committed is by taking the ratio of area of triangles wrongly. Instead of taking the area of $\Delta AXY=\dfrac{1}{2}$ area of $\Delta ABC$, you might take the area of $\Delta AXY=2$ (area of $\Delta ABC$).
Complete step-by-step answer:

It is given in the question that $ABC$ is a triangle in which $XY$||$BC$ and it divides the area of $\Delta ABC$ into two equal parts. Then, we have to find the value of $\left( \dfrac{BX}{AB} \right)$.

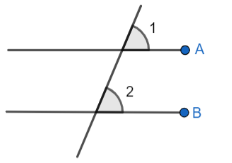
Here, in $\Delta ABC$ side $BC$ is parallel to $XY$. We know that, when two lines are parallel to each other and if a third line passes through both the lines then it is called a transverse line. And the angles made by the parallel and transverse lines are known to be transverse angles.

Since, $\angle 1=\angle 2$ as they are transverse angles. Now, in $\Delta ABC$, we have side$XY$||side$BC$. And side $AB$ and $AC$ are transverse lines for $XY$ and $BC$. So, when $XY$||$BC$ and $AB$ is a transversal line. Then, we get
$\angle AXY=\angle ABC$ ……….(i)
Both are corresponding angles and when $XY$||$BC$ and $AC$ is a transversal line. Then, we get
$\angle AYX=\angle ACB$ ………..(ii)
Then, $\Delta AXY$~$\Delta ABC$ by $AA$(ANGLE-ANGLE) similarity.
Now, we know that the ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides. So, we get
$\dfrac{ar(\Delta AXY)}{ar(\Delta ABC)}={{\left( \dfrac{AX}{AB} \right)}^{2}}$
We know that area of $\Delta AXY$=$\dfrac{1}{2}$ area of $\Delta ABC$. From this, we can write $ar(\Delta AXY)$ as $\dfrac{1}{2}ar(\Delta ABC)$
$\Rightarrow \dfrac{\dfrac{1}{2}ar(\Delta ABC)}{ar(\Delta ABC)}={{\left( \dfrac{AX}{AB} \right)}^{2}}$
Cancelling $ar(\Delta ABC)$ from numerator and denominator in L.H.S, we get
$\Rightarrow \dfrac{1}{2}={{\left( \dfrac{AX}{AB} \right)}^{2}}$
$\Rightarrow \dfrac{1}{\sqrt{2}}=\left( \dfrac{AX}{AB} \right)$ ……….(iii)
Now, we can write $AX$ as $(AB-BX)$ in equation (iii), we get
$\Rightarrow \dfrac{AB-BX}{AB}=\dfrac{1}{\sqrt{2}}$ ……….(iv)
On cross multiplying equation (iv), we get
$\Rightarrow \sqrt{2}(AB-BX)=1\times AB$
$\Rightarrow \sqrt{2}(AB-BX)=AB$
$\Rightarrow \sqrt{2}AB-\sqrt{2}BX=AB$
Transposing $-\sqrt{2}BX$ from L.H.S to R.H.S, we get
$\Rightarrow \sqrt{2}AB=AB+\sqrt{2}BX$
Transposing $AB$ from R.H.S to L.H.S, we get
$\Rightarrow \sqrt{2}AB-AB=\sqrt{2}BX$
Taking $AB$ as common in L.H.S, we get
$\Rightarrow AB(\sqrt{2}-1)=\sqrt{2}BX$
$\Rightarrow \sqrt{2}BX=(\sqrt{2}-1)AB$
On dividing by $\sqrt{2}AB$ on both the sides, we get
$\Rightarrow \dfrac{\sqrt{2}BX}{\sqrt{2}AB}=\dfrac{(\sqrt{2}-1)AB}{\sqrt{2}AB}$
$\Rightarrow \dfrac{BX}{AB}=\dfrac{\sqrt{2}-1}{\sqrt{2}}$
Note: You can solve this question by any method of your choice but, the key is you need to know that both $\Delta ABC$ and $\Delta AXY$ are similar to each other. The only possible mistake that can be committed is by taking the ratio of area of triangles wrongly. Instead of taking the area of $\Delta AXY=\dfrac{1}{2}$ area of $\Delta ABC$, you might take the area of $\Delta AXY=2$ (area of $\Delta ABC$).
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Computer Science: Engaging Questions & Answers for Success

Class 10 Question and Answer - Your Ultimate Solutions Guide

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
Who is known as the "Little Master" in Indian cricket history?

A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

State and explain Ohms law class 10 physics CBSE

Distinguish between soap and detergent class 10 chemistry CBSE

a Why did Mendel choose pea plants for his experiments class 10 biology CBSE

Draw the diagram of the sectional view of the human class 10 biology CBSE




